
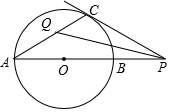
 如图,P是⊙O的直线AB的延长线上的一点,PC与⊙O相切于点C,∠APC的角平分线交AC于点Q,则∠PQC=45°.
如图,P是⊙O的直线AB的延长线上的一点,PC与⊙O相切于点C,∠APC的角平分线交AC于点Q,则∠PQC=45°. 分析 首先连接BC交PQ于E,由PC与圆D相切于点C,根据弦切角定理,即可得∠PCB=∠A,又由AB为直径,即可得∠ACB=90°,然后由PQ平分∠APC与三角形外角的性质(∠CQP=∠A+∠APQ,∠CEQ=∠PCB+∠QPC),即可证得∠CQP=CEQ,则可求得∠PQC的度数.
解答 解:解:连接BC交PQ于E,
∵PC与圆D相切于点C,
∴∠PCB=∠A,
∵AB为直径,
∴∠ACB=90°,
∵PQ平分∠APC,
∴∠APQ=∠QPC,
∵∠CQP=∠A+∠APQ,∠CEQ=∠PCB+∠QPC,
∴∠CQP=∠CEQ=$\frac{180°-90°}{2}$=45°.
故答案为45
点评 此题考查了圆的切线的性质,圆周角的性质,弦切角定理,等腰直角三角形的性质,以及三角形外角的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
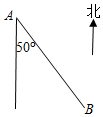 如图,货轮A与灯塔B相距20km,下列灯塔B相对于货轮A的位置的描述中,正确的是( )
如图,货轮A与灯塔B相距20km,下列灯塔B相对于货轮A的位置的描述中,正确的是( )| A. | 南偏东50° | B. | 南偏东50°且距货轮20 km处 | ||
| C. | 距灯塔20 km处 | D. | 北偏西50°且距货轮20 km处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2ab2-2b2 | B. | 2a2b-2b3 | C. | 2ab2+2b2 | D. | 2ab-2ab2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
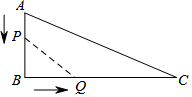 如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿BC边向C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,设运动时间为t,△PBQ的面积为S.
如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿BC边向C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,设运动时间为t,△PBQ的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com