练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知如图等腰，，，于点.点是延长线上一点，点是线段上一点，，下面的结论：①平分；②；③是等边三角形；④.其中正确的序号是________.

    【答案】①③④

    【解析】

    ①利用等边对等角，即可证得；

    ②因为点O是线段AD上一点，所以BO不一定是的角平分线，可作判断；

    ③证明且OP=OC，即可证得是等边三角形；

    ④首先证明,则AO=CE，AC=AE+CE=AO+AP；

    ∵，，

    ∴AD平分∴

    ∴平分 ①正确；

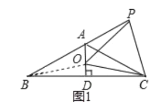
    如图1，连接BO，∵AD垂直平分BC

    ∴OB=OC 又∵OC=OP

    ∴OB=OC=OP

    ∴

    ∵点O在线段AD上，∴与不一定相等，

    则与不一定相等，故②不正确；

    ∵

    ∴

    ∵

    ∴

    ∴

    又∵OP=OC

    ∴是等边三角形，故③正确；

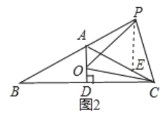
    如图2，在AC上截取AE=PA，连接PB，

    ∵

    ∴是等边三角形

    ∴

    ∴

    ∵

    ∴

    ∵OP=CP

    ∴

    ∴AO=CE

    ∴AC=AE+CE=AO+AP,故④正确；

    本题正确的结论有：①③④

    故答案为：①③④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在y轴上运动．

    （1）求直线AB的函数解析式；

    （2）动点M在y轴上运动，使MA+MB的值最小，求点M的坐标；

    （3）在y轴的负半轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司对一款新高压锅进行测试，放入足量的水和设定某一模式后，在容积不变的情况下，根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小．压强在加热前是100kpa，达到最大值后高压锅停止加热。为方便分析，测试员记y=p-100，

    表示压强在测试过程中相对于100kpa的增加值．部分数据如下表：

    温度f(℃)

    0

    10

    20

    30

    40

    50

    60

    压强增加值

    Y(kpa)

    0

    9.5

    18

    25.5

    32

    37.5

    42

    （1）根据表中的数据，在给出的坐标系中画出相应的点(坐标系已画在答卷上)；

    （2）y与t之问是否存在函数关系?若是，请求出函数关系式；否则请说明理由；

    （3）①在该模式下，压强P的最大值是多少?

    ②当t分别为，t1，t2(t1<t2)时，对应y的值分别为y1 ，y2 ， 请比较与的大小，并解释比较结果的实际意义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小华根据学习函数的经验，对函数的图象与性质进行了研究，下面是小华的研究过程，请补充完成.

    （1）自变量的取值范围是全体实数，与的几组对应值列表如下：

    4

    5

    m

    2

    1

    0

    n

    2

    3

    其中，m= ,n= ；

    （2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出该函数的图象；

    （3）观察图象，写出该函数的两条性质；

    （4）进一步研究函数图象发现：

    ①方程有 个实数根；

    ②不等式的解集为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，将一副直角三角板放在同一条直线AB上，其中∠ONM＝30°，∠OCD＝45°．

    （1）将图①中的三角板OMN沿BA的方向平移至图②的位置，MN与CD相交于点E，求∠CEN的度数；

    （2）将图①中的三角板OMN绕点O按逆时针方向旋转至如图③，当∠CON=5∠DOM时，MN与CD相交于点E，请你判断MN与BC的位置关系，并求∠CEN的度数；

    （3）将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周，在旋转的过程中，三角板MON运动几秒后直线MN恰好与直线CD平行．

    （4）将如图①位置的两块三角板同时绕点O逆时针旋转，速度分别每秒20°和每秒10°，当其中一个三角板回到初始位置时，两块三角板同时停止转动．经过___________秒后边OC与边ON互相垂直．（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的50%标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．

    （1）求该型号自行车的进价和标价分别是多少元？

    （2）若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上两点所表示的数分别为和，且满足，为原点．

    （1）试求和的值；

    （2）点从点出发向右运动，经过3秒后点到点的距离是点到点距离的3倍，求点的运动速度？

    （3）点以一个单位每秒的速度从点向右运动，同时点从点出发以5个单位每秒的速度向左运动，点从点出发，以20个单位每秒的速度向右运动．在运动过程中，分别为的中点，问的值是否发生变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A、B两地相距4km，上午8：00时，亮亮从A地步行到B地，8：20时芳芳从B地出发骑自行车到A地，亮亮和芳芳两人离A地的距离S（km）与亮亮所用时间t（min）之间的函数关系如图所示，芳芳到达A地时间为（ ）

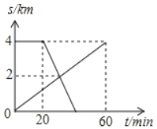
    A. 8：30 B. 8：35 C. 8：40 D. 8：45

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，、、分别为数轴上的三个点，点对应的数为60，点在点的左侧，并且与点的距离为30，点在点左侧，点到距离是点到点距离的4倍．

    （1）求出数轴上点对应的数及的距离．

    （2）点从点出发，以3单位/秒的速度项终点运动，运动时间为秒．

    ①点点在之间运动时，则_______．（用含的代数式表示）

    ②点在点向点运动过程中，何时、、三点中其中一个点是另外两个点的中点？求出相应的时间．

    ③当点运动到点时，另一点以5单位/秒速度从点出发，也向点运动，点到达点后立即原速返回到点，那么点在往返过程中与点相遇几次？直接写出相遇是点在数轴上对应的数．

    查看答案和解析>>

    同步练习册答案