
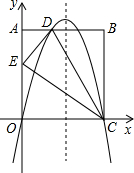
 ��ͼ���ھ���OABC�У�AO=10��AB=8����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��������y=ax2+bx+c����O��D��C���㣮
��ͼ���ھ���OABC�У�AO=10��AB=8����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��������y=ax2+bx+c����O��D��C���㣮���� ��1�������۵�ͼ�ε���Գ��ԣ���CED����CBDȫ�ȣ�������Rt��CEO�����OE�ij��������ɵõ�AE�ij�����Rt��AED�У�AD=AB-BD��ED=BD�����ù��ɶ��������AD�ij�����һ����ȷ��D�����꣬���ô���ϵ����������������ߵĽ���ʽ��
��2�����ڡ�DEC=90�㣬������ȷ�����ǡ�AED=��OCE������P��Q��CΪ��������������ADE���ƣ���ô��QPC=90����PQC=90�㣬Ȼ��������������£��ֱ��������������εĶ�Ӧ�߳ɱ��������Ӧ��t��ֵ��
��3��ֱ�����öԳƵ�����ʵó�M��λ�ã������ó��𰸣�
��� �⣺��1�����ı���ABCOΪ���Σ�
���OAB=��AOC=��B=90�㣬AB=CO=8��AO=BC=10��
�����⣬��BDC�ա�EDC��
���B=��DEC=90�㣬EC=BC=10��ED=BD��
�ɹ��ɶ�����EO=6��
��AE=10-6=4��
��AD=x����BD=ED=8-x���ɹ��ɶ�������x2+42=��8-x��2��
��ã�x=3����AD=3��
��������y=ax2+bx+c����D��3��10����C��8��0����O��0��0��
��$\left\{\begin{array}{l}{9a+3b=10}\\{64a+8b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{16}{3}}\end{array}\right.$
�������ߵĽ���ʽΪ��y=-$\frac{2}{3}$x2+$\frac{16}{3}$x��
��2���ߡ�DEA+��OEC=90�㣬��OCE+��OEC=90�㣬
���DEA=��OCE��
�ɣ�1���ɵ�AD=3��AE=4��DE=5��
��CQ=t��EP=2t����PC=10-2t��
����PQC=��DAE=90�㣬��ADE�ס�QPC��
��$\frac{CQ}{AE}$=$\frac{CP}{DE}$����$\frac{t}{4}$=$\frac{10-2t}{5}$��
��ã�t=$\frac{40}{13}$��
����QPC=��DAE=90�㣬��ADE�ס�PQC��
��$\frac{PC}{AE}$=$\frac{QC}{DE}$����$\frac{10-2t}{4}$=$\frac{t}{5}$��
��ã�t=$\frac{25}{7}$��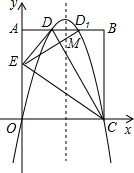
�൱t=$\frac{40}{13}$��$\frac{25}{7}$ʱ����P��Q��CΪ��������������ADE���ƣ�
��3����ͼ��ʾ������D��3��10�����ڶԳ���x=4�ĶԳƵ�D1��5��10��������D1E���Գ���x=4�ڵ�M����ʱMD+ME��ֵ��С��
��ֱ��D1E�Ľ���ʽΪ��y=kx+b��k��0����
��E��0��6����D1��5��10������ã�$\left\{\begin{array}{l}{b=6}\\{5k+b=10}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{4}{5}}\\{b=6}\end{array}\right.$��
��ֱ��D1E�Ľ���ʽΪ��y=$\frac{4}{5}$x+6��0��x��5����
��x=4����ã�y=$\frac{46}{6}$��
��M��4��$\frac{46}{5}$����
��ʱ��MD+ME=ME+MD1=D1E=$\sqrt{A{E}^{2}+A{D}^{2}}$=$\sqrt{41}$��
���� ���⿼���˶��κ����ۺ��⣬��Ŀ�漰��ͼ�ε��۵��任�����������ε��ж������ʡ�ƽ���ı��ε��ж������ʵ��ص�֪ʶ����2����Ҫ���з������ۣ�����©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4x2-1 | B�� | 2x2-1 | C�� | 4x-1 | D�� | 4x2+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
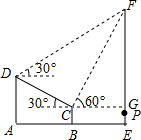 ��ͼ��ijУ��������һ��̨�Ľ���ͼ����̨CD��ˮƽ�ߵļн�Ϊ30�㣬��ʹ�C�����ľ���BCΪ2.5�ף���C��D��ǰ���д�ֱ�ڵ�������EF����C��D���������˶���F�����Ƿֱ�Ϊ60���30�㣬CD��Ϊ10�ף�������ʽ�У������迪ʼ����ʱ������Ҳ�������1.5��P��ͬʱȽȽ���𣬹��貥�Ž���ʱ������պ���������˶���F����֪���貥��ʱ��Ϊ46�룬�����������ƽ���ٶȣ��������ȷ��0.01��/�룩
��ͼ��ijУ��������һ��̨�Ľ���ͼ����̨CD��ˮƽ�ߵļн�Ϊ30�㣬��ʹ�C�����ľ���BCΪ2.5�ף���C��D��ǰ���д�ֱ�ڵ�������EF����C��D���������˶���F�����Ƿֱ�Ϊ60���30�㣬CD��Ϊ10�ף�������ʽ�У������迪ʼ����ʱ������Ҳ�������1.5��P��ͬʱȽȽ���𣬹��貥�Ž���ʱ������պ���������˶���F����֪���貥��ʱ��Ϊ46�룬�����������ƽ���ٶȣ��������ȷ��0.01��/�룩�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
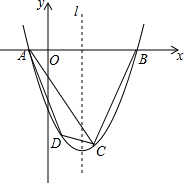 ��ͼ����֪���κ�����ͼ��M����A��-1��0����B��4��0����C��2��-6�����㣮
��ͼ����֪���κ�����ͼ��M����A��-1��0����B��4��0����C��2��-6�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
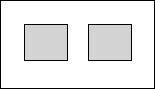 ij�㳡�̻���������һ�鳤2ǧ�ף���1ǧ�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ������̵�֮����ܱ����п�����ȵ�����ͨ������ͼ����������Щ����ͨ�����ϴ�ש��Ҫ���̴�ש������Ǿ��οյ������$\frac{1}{2}$��������ͨ���Ŀ���Ϊxǧ�ף������з�����ȷ���ǣ�������
ij�㳡�̻���������һ�鳤2ǧ�ף���1ǧ�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ������̵�֮����ܱ����п�����ȵ�����ͨ������ͼ����������Щ����ͨ�����ϴ�ש��Ҫ���̴�ש������Ǿ��οյ������$\frac{1}{2}$��������ͨ���Ŀ���Ϊxǧ�ף������з�����ȷ���ǣ�������| A�� | ��2-3x����1-2x��=1 | B�� | $\frac{1}{2}$��2-3x����1-2x��=1 | C�� | $\frac{1}{4}$��2-3x����1-2x��=1 | D�� | $\frac{1}{4}$��2-3x����1-2x��=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com