
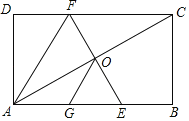
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:
①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG=![]() S△ABC
S△ABC
其中正确的是______.(把所有正确结论的序号都选上)
【答案】①②④.
【解析】试题分析:根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=![]() AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
由∠AFC=120°,∠FCA=30°,可知∠AFE=60°,因此△AEF是等边三角形,故②正确;
连接CE,则根据三角形的中位线可知CE=2OG,由矩形的性质可得四边形AECF是菱形,且![]() ,由OE=OG,OA=
,由OE=OG,OA=![]() AC,可知
AC,可知![]() ,解得AC=
,解得AC=![]() OG,故③不正确;
OG,故③不正确;
令AE=2a,则OG=OE=a,AO=![]() a,AC=2
a,AC=2![]() a,由S△AOE=
a,由S△AOE=![]() ×a×
×a×![]() a=
a=![]() 2,S矩形ABCD=3a×
2,S矩形ABCD=3a×![]() a=3
a=3![]() a2 ,即S△AOG=
a2 ,即S△AOG=![]() S△ABC,故④正确.
S△ABC,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.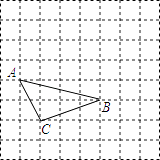
(1)画出直角坐标系;
(2)画出与△ABC关于x轴对称的图形△DEF;
(3)P为x轴上的一个动点,是否存在P使PA+PB的值最小?若不存在,请说明理由;若存在请求出点P的坐标和PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
频数 | 16 | 25 | 9 | 7 | 3 |
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中:
①两条对角线互相平分且相等的四边形是菱形;
②菱形的一条对角线平分一组对角;
③若三条线段平方之比是1:1:2,则它们组成一个等腰直角三角形;
④两条对角线互相平分的四边形是矩形;
⑤平行四边形对角线相等.
真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com