
 观察下面由“※”组成的图案(如图)及算式,解答下列问题:
观察下面由“※”组成的图案(如图)及算式,解答下列问题:分析 (1)根据给定等式的变化,即可得出1+3+5+7+9+…+19的值;
(2)根据给定等式的变化,即可得出变化规律“1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=$(\frac{2n+3+1}{2})^{2}$=(n+2)2”,依次规律即可得出结论;
(3)根据(2)的结论,即可得出1001+1003+1005+…+2011+2013=$(\frac{2013+1}{2})^{2}$-$(\frac{999+1}{2})^{2}$,此题得解.
解答 解:(1)∵1+3=22=$(\frac{3+1}{2})^{2}$,1+3+5=32=$(\frac{5+1}{2})^{2}$,1+3+5+7=42=$(\frac{7+1}{2})^{2}$,1+3+5+7+9=52=$(\frac{9+1}{2})^{2}$,
∴1+3+5+7+9+…+19=$(\frac{19+1}{2})^{2}$=100.
(2)∵1+3=22=$(\frac{3+1}{2})^{2}$,1+3+5=32=$(\frac{5+1}{2})^{2}$,1+3+5+7=42=$(\frac{7+1}{2})^{2}$,1+3+5+7+9=52=$(\frac{9+1}{2})^{2}$,…,
∴1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=$(\frac{2n+3+1}{2})^{2}$=(n+2)2.
(3)1001+1003+1005+…+2011+2013=(1+3+5+…+2013)-(1+3+5+…+999)=$(\frac{2013+1}{2})^{2}$-$(\frac{999+1}{2})^{2}$=764049.
点评 本题考查了规律型中数字的变化,根据等式的变化找出变化规律是解题的关键.


科目:初中数学 来源: 题型:填空题
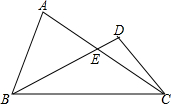 如图,已知△ABC中,AC=BC,点D在△ABC外,且点D在AC的垂直平分线上,连接BD,BD与AC相交于点E,若∠DBC=30°,∠ACD=11°,则∠A=71度.
如图,已知△ABC中,AC=BC,点D在△ABC外,且点D在AC的垂直平分线上,连接BD,BD与AC相交于点E,若∠DBC=30°,∠ACD=11°,则∠A=71度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com