
ΓΨΧβΡΩΓΩ»γΆΦΘ§P «œΏΕΈAB…œ“ΜΒψΘ§ABΘΫ12cmΘ§CΓΔDΝΫΒψΖ÷±π¥”PΓΔB≥ωΖΔ“‘1cm/sΓΔ2cm/sΒΡΥΌΕ»Ά§ ±―Ί÷±œΏABœρΉσ‘ΥΕ·Θ®C‘ΎœΏΕΈAP…œΘ§D‘ΎœΏΕΈBP…œΘ©Θ§‘ΥΕ· ±ΦδΈΣts
Θ®IΘ©»τCΓΔD‘ΥΕ·1s ±Θ§«“PDΘΫ2ACΘ§«σAPΒΡ≥ΛΘΜ
Θ®IIΘ©»τCΓΔD‘ΥΕ·ΒΫ»Έ“Μ ±ΩΧ ±Θ§Ήή”–PDΘΫ2ACΘ§APΒΡ≥ΛΕ» «Ζώ±δΜ·ΘΩ»τ≤Μ±δΘ§«κ«σ≥ωAPΒΡ≥ΛΘΜ»τ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ
Θ®IIIΘ©‘ΎΘ®IIΘ©ΒΡΧθΦΰœ¬Θ§Q «÷±œΏAB…œ“ΜΒψΘ§«“AQ©¹BQΘΫPQΘ§«σPQΒΡ≥ΛΘ°
![]()
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©PAΘΫ4cmΘΜΘ®ΔρΘ©≥ΛΕ»≤ΜΖΔ…ζ±δΜ·Θ§APΘΫ4cmΘ§Θ®ΔσΘ©PQΘΫ4cmΜρ12cmΘ°
ΓΨΫβΈωΓΩ
Θ®ΔώΘ©”…AC+CP+PD+BDΘΫABΘ§Ν–≥ωΖΫ≥ΧΩ…«σACΒΡ≥ΛΘ§Φ¥Ω…«σΫβΘΜ
Θ®ΔρΘ©”…œΏΕΈΒΡΚΆ≤νΙΊœΒΩ…«σΫβΘΜ
Θ®ΔσΘ©”…Χβ…ηΜ≠≥ωΆΦ ΨΘ§ΗυΨίAQ©¹BQΘΫPQ«σΒΟAQΘΫPQ+BQΘΜ»ΜΚσ«σΒΟAPΘΫBQΘ§¥”Εχ«σΒΟPQ”κABΒΡΙΊœΒΘ°
ΫβΘΚΘ®ΔώΘ©ΗυΨίCΓΔDΒΡ‘ΥΕ·ΥΌΕ»Ω…÷ΣΘΚBDΘΫ2cmΘ§PCΘΫ1cmΘ§
ΓΏAC+CP+PD+BDΘΫABΘ§«“PDΘΫ2ACΘ§
ΓύAC+1+2AC+2ΘΫ12Θ§
ΓύACΘΫ3cmΘ§
ΓύPAΘΫ4ccmΘΜ
Θ®ΔρΘ©≥ΛΕ»≤ΜΖΔ…ζ±δΜ·Θ§
άμ”…»γœ¬ΘΚ
ΗυΨίCΓΔDΒΡ‘ΥΕ·ΥΌΕ»Ω…÷ΣΘΚBDΘΫ2PCΘ§
ΓΏAC+CP+PD+BDΘΫABΘ§«“PDΘΫ2ACΘ§
Γύ3AC+3PCΘΫ12Θ§
ΓύAPΘΫ4cmΘ§
Θ®ΔσΘ©»γΆΦΘΚ
![]()
ΓΏAQ©¹BQΘΫPQΘ§
ΓύAQΘΫPQ+BQΘΜ
”÷ΓΏAQΘΫAP+PQΘ§
ΓύAPΘΫBQΘ§
ΓύPQΘΫ![]() ABΘΫ4cmΘΜ
ABΘΫ4cmΘΜ
Β±ΒψQ'‘ΎABΒΡ―”≥ΛœΏ…œ ±Θ§
AQΓδ©¹APΘΫPQΓδΘ§
Υυ“‘AQΓδ©¹BQΓδΘΫPQΘΫABΘΫ12cmΘ°
Ήέ…œΥυ ωΘ§PQΘΫ4cmΜρ12cmΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏΫΜ”ΎΒψOΘ§ΒψEΓΔFΖ÷±π‘ΎABΓΔBC…œΘ®AEΘΦBEΘ©Θ§
«“ΓœEOFΘΫ90ΓψΘ§OEΓΔDAΒΡ―”≥ΛœΏΫΜ”ΎΒψMΘ§OFΓΔABΒΡ―”≥ΛœΏΫΜ”ΎΒψNΘ§Ν§Ϋ”MNΘ°
Θ®1Θ©«σ÷ΛΘΚOMΘΫONΘΜ
Θ®2Θ©»τ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ6Θ§OEΘΫEMΘ§«σMNΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–Ϋα¬έΘΚΔΌΦΗΗω”–άμ ΐœύ≥ΥΘ§»τΤδ÷–ΗΚ“ρ ΐ”–Τφ ΐΗωΘ§‘ρΜΐΈΣΗΚΘΜΔΎΝΫΗω»ΐ¥ΈΕύœν ΫΒΡΚΆ“ΜΕ® «»ΐ¥ΈΕύœν ΫΘΜΔέ»τxyzΘΦ0Θ§‘ρ![]() +
+![]() +
+![]() +
+![]() ΒΡ÷ΒΈΣ0Μρ©¹4ΘΜΔή»τaΘ§bΜΞΈΣœύΖ¥ ΐΘ§‘ρ
ΒΡ÷ΒΈΣ0Μρ©¹4ΘΜΔή»τaΘ§bΜΞΈΣœύΖ¥ ΐΘ§‘ρ![]() ΘΫ©¹1ΘΜΔί»τxΘΫyΘ§‘ρ
ΘΫ©¹1ΘΜΔί»τxΘΫyΘ§‘ρ![]() ΘΫ
ΘΫ![]() Θ°Τδ÷–’ΐ»ΖΒΡΗω ΐ”–Θ®ΓΓΓΓΘ©
Θ°Τδ÷–’ΐ»ΖΒΡΗω ΐ”–Θ®ΓΓΓΓΘ©
A.1ΗωB.2ΗωC.3ΗωD.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§“―÷ΣABΓΈCDΘ§ADΓΈBCΘ§AC”κBDΫΜ”ΎΒψOΘ§AEΓΆBD”ΎEΘ§CFΓΆBD”ΎEΘ§ΆΦ÷–»ΪΒ»»ΐΫ«–Έ”–Θ®ΓΓΓΓΘ©

A. 3Ε‘ B. 5Ε‘ C. 6Ε‘ D. 7Ε‘
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩAΓΔBΝΫΝΨΤϊ≥ΒΆ§ ±¥”œύΨύ330«ßΟΉΒΡΦΉΓΔ““ΝΫΒΊœύœρΕχ––Θ§sΘ®«ßΟΉΘ©±μ ΨΤϊ≥Β”κΦΉΒΊΒΡΨύάκΘ§tΘ®Ζ÷Θ©±μ ΨΤϊ≥Β–– ΜΒΡ ±ΦδΘ§»γΆΦΘ§L1Θ§L2Ζ÷±π±μ ΨΝΫΝΨΤϊ≥ΒΒΡs”κtΒΡΙΊœΒΘ°
Θ®1Θ©L1±μ ΨΡΡΝΨΤϊ≥ΒΒΫΦΉΒΊΒΡΨύάκ”κ–– Μ ±ΦδΒΡΙΊœΒΘΩ
Θ®2Θ©Τϊ≥ΒBΒΡΥΌΕ» «Εύ…ΌΘΩ
Θ®3Θ©«σL1Θ§L2Ζ÷±π±μ ΨΒΡΝΫΝΨΤϊ≥ΒΒΡs”κtΒΡΙΊœΒ ΫΘ°
Θ®4Θ©2–Γ ±ΚσΘ§ΝΫ≥ΒœύΨύΕύ…Ό«ßΟΉΘΩ
Θ®5Θ©–– ΜΕύ≥Λ ±ΦδΚσΘ§AΓΔBΝΫ≥Βœύ”ωΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΙΐAΒψΒΡ“Μ¥ΈΚ· ΐΒΡΆΦœσ”κ’ΐ±»άΐΚ· ΐyΘΫ2xΒΡΆΦœσœύΫΜ”ΎΒψB.
(1)«σ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
(2)≈–ΕœΒψC(4Θ§Θ≠2) «Ζώ‘ΎΗΟ“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ§ΥΒΟςάμ”…ΘΜ
(3)»τΗΟ“Μ¥ΈΚ· ΐΒΡΆΦœσ”κx÷αΫΜ”ΎDΒψΘ§«σΓςBODΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΈΣΑκ‘≤OΒΡ÷±ΨΕΘ§AC «Γ―OΒΡ“ΜΧθœ“Θ§DΈΣ![]() ΒΡ÷–ΒψΘ§ΉςDEΓΆACΘ§ΫΜABΒΡ―”≥ΛœΏ”ΎΒψFΘ§Ν§Ϋ”DAΘ°
ΒΡ÷–ΒψΘ§ΉςDEΓΆACΘ§ΫΜABΒΡ―”≥ΛœΏ”ΎΒψFΘ§Ν§Ϋ”DAΘ°
Θ®1Θ©«σ÷ΛΘΚEFΈΣΑκ‘≤OΒΡ«–œΏΘΜ
Θ®2Θ©»τDA=DF=![]() Θ§«σ“θ”Α«χ”ρΒΡΟφΜΐΘ°Θ®ΫαΙϊ±ΘΝτΗυΚ≈ΚΆΠ–Θ©
Θ§«σ“θ”Α«χ”ρΒΡΟφΜΐΘ°Θ®ΫαΙϊ±ΘΝτΗυΚ≈ΚΆΠ–Θ©

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ΫΒΊΉ‘––≥Β‘Ϋά¥‘Ϋ ήΒΫ÷–―ß…ζΒΡœ≤Α°Θ§Ης÷÷ΤΖ≈ΤœύΦΧΆΕΖ≈ –≥ΓΘ§Ρ≥≥Β––Ψ≠”ΣΒΡA–Ά≥Β»ΞΡξœζ έΉήΕνΈΣ5Άρ‘ΣΘ§ΫώΡξΟΩΝΨœζ έΦέ±»»ΞΡξΫΒΒΆ400‘ΣΘ§»τ¬τ≥ωΒΡ ΐΝΩœύΆ§Θ§œζ έΉήΕνΫΪ±»»ΞΡξΦθ…Ό20%Θ°
Θ®1Θ©ΫώΡξA–Ά≥ΒΟΩΝΨ έΦέΕύ…Ό‘ΣΘΩΘ®”ΟΝ–ΖΫ≥ΧΒΡΖΫΖ®Ϋβ¥πΘ©
Θ®2Θ©ΗΟ≥Β––ΦΤΜ°–¬Ϋχ“Μ≈ζA–Ά≥ΒΚΆ–¬ΩνB–Ά≥ΒΙ≤60ΝΨΘ§«“B–Ά≥ΒΒΡΫχΜθ ΐΝΩ≤Μ≥§ΙΐA–Ά≥Β ΐΝΩΒΡΝΫ±ΕΘ§”Π»γΚΈΫχΜθ≤≈Ρή Ι’β≈ζ≥ΒΜώάϊΉνΕύΘΩ
AΘ§BΝΫ÷÷–ΆΚ≈≥ΒΒΡΫχΜθΚΆœζ έΦέΗώ»γœ¬±μΘΚ
A–Ά≥Β | B–Ά≥Β | |
ΫχΜθΦέΗώΘ®‘ΣΘ© | 1100 | 1400 |
œζ έΦέΗώΘ®‘ΣΘ© | ΫώΡξΒΡœζ έΦέΗώ | 2000 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§OAΓΆOBΘ§“ΐ…δœΏOCΘ®ΒψC‘ΎΓœAOBΆβΘ©Θ§»τΓœBOCΘΫΠΝΘ®0ΓψΘΦΠΝΘΦ90ΓψΘ©Θ§
ODΤΫΓœBOCΘ§OEΤΫΓœAODΘ°
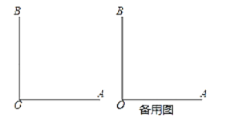
Θ®1Θ©»τΠΝΘΫ40ΓψΘ§«κ“άΧβ“β≤Ι»ΪΆΦ–ΈΘ§≤Δ«σΓœBOEΒΡΕ» ΐΘΜ
Θ®2Θ©«κΗυΨίΓœBOCΘΫΠΝΘ§«σ≥ωΓœBOEΒΡΕ» ΐΘ®”ΟΚ§ΠΝΒΡ±μ ΨΘ©.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com