
【题目】如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。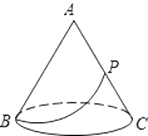
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。(结果不取近似数)
【答案】
(1)解:∵主视图是边长为6m的正三形ABC,
∴AB母线AB=R=6m,
∴底面圆的半径r=3m,
∴S侧=![]() rR=
rR=![]() ×3×6=18
×3×6=18![]() (m2),
(m2),
(2)解:∵△ABC为正三角形,
∴BC=6,
∴l=2π×3=6π,
根据底面圆的周长等于展开后扇形的弧长,得: ![]() =6π,
=6π,
故n=180°,则∠BAC=90°,
∴BP= ![]() =3
=3 ![]() m
m
答:小猫所经过的最短路程是3 ![]() m.
m.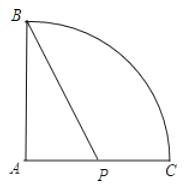
【解析】(1)由圆锥的侧面展开图是扇形,再根据圆锥的侧面积公式=![]()
![]() ×r×R计算即可.
×r×R计算即可.
(2)根据两点之间,线段最短;依题可得展开的是圆锥的半个侧面,再连接BP,再根据勾股定理计算即可.
【考点精析】利用弧长计算公式和扇形面积计算公式对题目进行判断即可得到答案,需要熟知若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A,B的俯角∠DCA=45°、∠DCB=30°(己知A,B,C三点在同一平面上),求钓鱼岛南北两端A,B的距离.(参考数据: ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
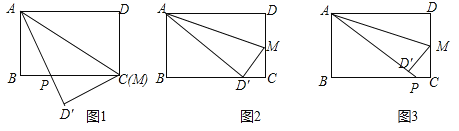
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在![]() 中,点
中,点![]() 是
是![]() 、
、![]() 的平分线的交点,点
的平分线的交点,点![]() 是
是![]() 、
、![]() 平分线的交点,
平分线的交点,![]() 的延长线交于点
的延长线交于点![]() .
.

(1)若![]() ,则
,则![]() °;
°;
(2)若![]() (
(![]() ),则当
),则当![]() 等于多少度(用含
等于多少度(用含![]() 的代数式表示)时,
的代数式表示)时,![]() ,并说明理由;
,并说明理由;
(3)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 . 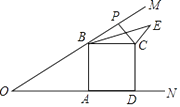
查看答案和解析>>
科目:初中数学 来源: 题型:
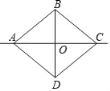
【题目】如图,四边形ABCD沿直线AC对折后重合,如果AC,BD交于O,AB∥CD,则结论①AB=CD,②AD∥BC,③AC⊥BD,④AO=CO,⑤AB⊥BC,其中正确的结论是___(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=32°,则∠ACF的度数为__________°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com