(1)解:AO=BO,DH=EH,DF=AF,AC=DE;
(2)证明:连EC,AE,
则∠PFC是△ECF的一个外角,于是∠PFC=∠ACE+∠FEC;
∵DH⊥AB,AB是⊙O的直径,
∴A是DE中点,即弧AD=弧AE,
∴∠AED=∠ACE,
∴∠ACE+∠FEC=∠AED+∠DEC=∠AEC,
∵PC是⊙O的切线,
∴∠PCA=∠AEC.
∴∠PCA=∠PFC,
∴PC=PF.
∵PC是切线
∴PC
2=PD•PE,
∴PF
2=PD•PE;
(3)解:在⊙O中,AH•HB=DH•HE=DH
2,
∴
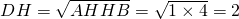
设AF=x,则FH=2-x.
在Rt△AFH中,AH
2+FH
2=AF
2∴1+(2-x)
2=x
2,
∴x=

,即

.
于是

.
由(1)(2)知HE=HD=2,
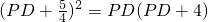
,
解得
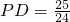
.
∴PF=PD+DF=
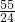
.
∴PC=PF=
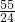
.
分析:(1)分别根据半径相等,垂径定理可知AO=BO,DH=EH;知道D是劣弧AC的中点,结合垂径定理可知弧AC等于弧DE,从而可得DF=AF,AC=DE;
(2)连EC,AE,由(1)可知弧AD=弧AE,分别利用等弧所对的圆周角相等和弦切角等于它所夹的弧对的圆周角可得到∠PCA=∠PFC,从而可知PC=PF,利用切割线定理可知PC
2=PD•PE,等量代换即可求解;
(3)先根据射影定理求得DH的长为2,结合前2问可设AF=x,则FH=2-x,利用Rt△AFH中AH
2+FH
2=AF
2,求得DF的长,再利用第2问的结论作为相等关系,即可求得PD的长,从而可求得PF,即PC的长.
点评:主要考查了圆中的有关定理:垂径定理,切割线定理,弦切角定理等.本题的解题关键是会运用方程思想把线段之间存在的数量关系(定理所体现的数量关系)作为相等关系列方程求线段的长度.

 出现在结论中,不必写出推理过程.)
出现在结论中,不必写出推理过程.)
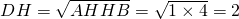
 ,即
,即 .
. .
.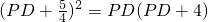 ,
,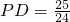 .
.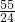 .
.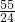 .
.

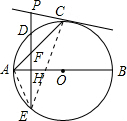
 25、如图,AB、AC分别为⊙O的直径和弦,D为劣弧AC上一点,DE⊥AB于H交⊙O于E,交AC于点F,P为ED延长线上的一点.
25、如图,AB、AC分别为⊙O的直径和弦,D为劣弧AC上一点,DE⊥AB于H交⊙O于E,交AC于点F,P为ED延长线上的一点.