
【题目】如图,已知△ABC和△BDE都是等边三角形。则下列结论:①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60.⑤△BFG是等边三角形,其中正确的有___.

【答案】①②④⑤
【解析】
由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60,
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD,故①正确
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60,
∴△BGD≌△BFE,
∴BG=BF,∠BFG=∠BGF=60,故②正确,
∴△BFG是等边三角形,故⑤正确,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60,
∴△ABF≌△CGB,
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,故④正确,
∵∠FGB=∠GBD=60°,
∴FG∥AD,
不妨设FG⊥BH,则BH⊥AD,易证△ABH≌△DBH,可得AB=BD,显然与已知条件矛盾,故③错误,
故答案为①②④⑤.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
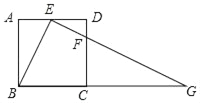
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
A.50B.-50C.60D.-60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点。
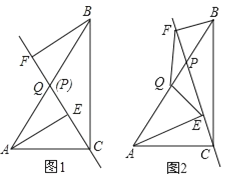
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___,QE与QF的数量关系是___;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠α的顶点在正n边形的中心点O处,∠α绕着顶点O旋转,角的两边与正n边 形的两边分别交于点M、N,∠α与正n边形重叠部分面积为S.
(1)当n=4,边长为2,∠α=90°时,如图(1),请直接写出S的值;

(2)当n=5,∠α=72°时,如图(2),请问在旋转过程中,S是否发生变化?并说明理由;

(3)当n=6,∠α=120°时,如图(3),请猜想S是原正六边形面积的几分之几(不必说明理由).若∠α的平分线与BC边交于点P,判断四边形OMPN的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.关于某直线对称的两个三角形是全等三角形B.全等三角形是关于某直线对称的
C.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧D.有一条公共边的两个全等三角形关于公共边所在的直线对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com