
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成“![]() ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
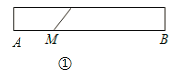

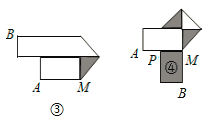
如果由信纸折成的长方形纸条(图①)长为2 6 厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BE=_____厘米; 在图④中,BM=______厘米.
(2)如果长方形纸条的宽为x厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(结果用x表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )

A. (3,-1) B. (-1,-1) C. (1,1) D. (-2,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从苏州出发,1日到4日在北京旅游,8月5日上午返回苏州.
苏州与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 (身高超过1.2米全票) |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)他们往返都坐飞机 (成人票五五折),其他开支不变,至少要准备多少元?
(3)他们去时坐火车,回来坐飞机 (成人票五五折),其他开支不变,准备了14000元,是否够用?如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知:如图,![]() 与
与![]() 互补,
互补,![]() ,
,
求证:![]()

证明:![]() 与
与![]() 互补
互补
即![]() ,(已知)
,(已知)
![]() // ( )
// ( )
![]() .( )
.( )
又![]() ,(已知)
,(已知)
![]() ,即
,即![]() .(等式的性质)
.(等式的性质)
![]() // (内错角相等,两直线平行)
// (内错角相等,两直线平行)
![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,
![]() 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.
②![]() 59319的个位数是9,又
59319的个位数是9,又![]() ,
,
![]() 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①![]() ;
;
②![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示.其中阅读时间是8~10小时的频数和频率分别是( )
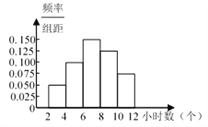
A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com