[题目]如图.在△ABC和△ADE中.AB=AC.AD=AE.且∠BAC=∠DAE.点E在BC上．过点D作DF∥BC.连接DB．求证:(1)△ABD≌△ACE,(2)DF=CE．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，点E在BC上．过点D作DF∥BC，连接DB．

求证：（1）△ABD≌△ACE；

（2）DF=CE．

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）求出∠BAD=∠BAC，根据SAS证出△BAD≌△CAE即可；

（2）根据全等推出∠DBA=∠C，根据等腰三角形性质得出∠C=∠ABC，根据平行线性质得出∠ABC=∠DFB，推出∠DFB=∠DBF，根据等腰三角形的判定推出即可．

（1）∵∠BAC=∠DAE，∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，∴∠BAD=∠EAC．在△BAD和△CAE中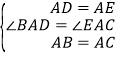，∵，∴△BAD≌△CAE（SAS）；

（2）∵△BAD≌△CAE，∴∠DBA=∠C．

∵AB=AC，∴∠C=∠ABC．

∵DF∥BC，∴∠DFB=∠ABC=∠C=∠DBA，即∠DFB=∠DBF，∴DF=CE．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】⑴ 阅读理解：我们知道在直角三角形中，有无数组勾股数，例如：5、12、13；9、40、41；……但其中也有一些特殊的勾股数，例如：3、4、5；是三个连续正整数组成的勾股数.

解决问题：① 在无数组勾股数中，是否存在三个连续偶数能组成勾股数？

答：，若存在，试写出一组勾股数： .

② 在无数组勾股数中，是否还存在其它的三个连续正整数能组成勾股数？若存在，求出勾股数，若不存在，说明理由.

③ 在无数组勾股数中，是否存在三个连续奇数能组成勾股数？若存在，求出勾股数，若不存在，说明理由.

⑵ 探索升华：是否存在锐角△ABC三边也为连续正整数；且同时还满足：∠B＞∠C＞∠A；∠ABC＝2∠BAC？若存在，求出△ABC三边的长；若不存在，说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】先化简，再求值：

(1)(x＋1)2＋x(x－2)，其中x＝－；

(2)[(xy＋2)(xy－2)－2(x2y2－2)]÷xy，其中x＝10，y＝－；

(3)已知a＋b＝12，ab＝20，求a(a＋b)(a－b)－a(a＋b)2的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=﹣ x2+bx+c表示，且抛物线的点C到墙面OB的水平距离为3m时，到地面OA的距离为 m．

（1）求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，在Rt△ABC中，∠ABC=90°，AB=BC，点D是AC的中点，直角∠EDF的两边分别交AB、BC于点E、F，给出以下结论：①AE=BF；②S四边形BEDF=S△ABC；③△DEF是等腰直角三角形；④当∠EDF在△ABC内绕顶点D旋转时D旋转时（点E不与点A、B重合），∠BFE=∠CDF，上述结论始终成立的有（　　）个．

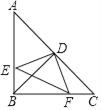
A. 1 B. 2 C. 3 D. 4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】先化简,再求值: ，其中x的值从不等式组的整数解中选取.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了庆祝建校八十周年，某校各班都在开展丰富多彩的庆祝活动，八年级(3)班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学制作手工作品的第一、二个步骤是：①先裁下了一张长BC＝20 cm，宽AB＝16 cm的长方形纸片ABCD；②将纸片沿着直线AE折叠，使点D恰好落在BC边上的F处……请你根据①②步骤解答下列问题．