
分析 (1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;
(3)原式变形后,利用平方差公式计算即可得到结果;
(4)原式利用完全平方公式,以及平方差公式计算,去括号合并即可得到结果.
解答 解:(1)原式=-6a3b+4a2b2+2ab3;
(2)原式=1+$\frac{1}{4}$-$\frac{1}{4}$+2013=2014;
(3)原式=(100+2)×(100-2)=10000-4=9996;
(4)原式=2m2+4m+2-4m2+1=-2m2+4m+3.
点评 此题考查了平方差公式,实数的运算,单项式乘多项式,完全平方公式,以及零指数幂、负整数指数幂法则,熟练掌握公式及法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
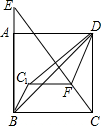 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用长32米的篱笆围成面积为130m2的矩形场地,矩形场地的一面利用墙可用最大长度为16m,与墙平行的对边有1m长的一道门,求此矩形场地的长、宽各是多少米?
用长32米的篱笆围成面积为130m2的矩形场地,矩形场地的一面利用墙可用最大长度为16m,与墙平行的对边有1m长的一道门,求此矩形场地的长、宽各是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com