
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
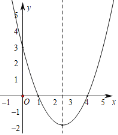
(1)求该抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.
【答案】(1)![]() ;(2)存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;(3)Q的坐标
;(2)存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;(3)Q的坐标![]() 或
或![]() .
.
【解析】
(1)将A(1,0)、B(4,0)、C(0,3)代入y=ax2+bx+c,求出a、b、c即可;
(2)四边形PAOC的周长最小值为:OC+OA+BC=1+3+5=9;
(3)分两种情况讨论:①当△BPQ∽△BCA,②当△BQP∽△BCA.
解:(1)由已知得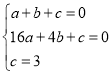 ,
,
解得 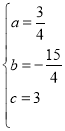
所以,抛物线的解析式为![]() ;
;
(2)∵A、B关于对称轴对称,如下图,连接BC,与对称轴的交点即为所求的点P,此时PA+PC=BC,
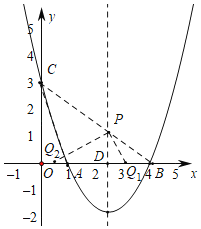
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;
(3)如上图,设对称轴与x轴交于点D.
∵A(1,0)、B(4,0)、C(0,3),
∴OB=4,AB=3,BC=5,
直线BC:![]() ,
,
由二次函数可得,对称轴直线![]() ,
,
∴![]() ,
,
①当△BPQ∽△BCA,
![]() ,
,
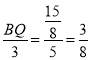 ,
,
![]() ,
,
![]() ,
,
![]()
②当△BQP∽△BCA,
![]() ,
,
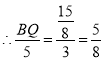 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上,求得点Q的坐标![]() 或
或![]()


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.

(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD- DC- CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
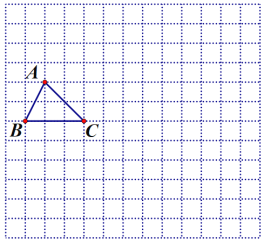
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度后得到△A1B1C1.画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2.画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且∠DAE=![]() α.
α.
(1)如图1,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF,
①求∠DAF的度数;
②求证:△ADE≌△ADF;
(2)如图2,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由;
(3)如图3,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论是( )
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论是( )
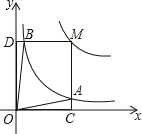
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com