
【题目】(2014河南22题)
(1)问题发现
如图①,![]() 和
和![]() 均为等边三角形,点A、D、E在同一条直线上,连接BE;
均为等边三角形,点A、D、E在同一条直线上,连接BE;
填空:
①![]() 的度数为__________;
的度数为__________;
②线段AD、BE之间的数量关系为__________.
(2)拓展探究
如图②,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点A、D、E在同一条直线上,CM为
,点A、D、E在同一条直线上,CM为![]() 中DE边上的高,连接BE.请判断
中DE边上的高,连接BE.请判断![]() 的度数及线段CM、AE、BE之间的数量关系,并说明理由;
的度数及线段CM、AE、BE之间的数量关系,并说明理由;
(3)解决问题
如图③,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点A到BP的距离.
,请直接写出点A到BP的距离.
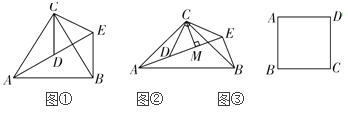
图① 图② 图③
【答案】(1)①60°;②![]() ;(2)①
;(2)①![]() ;②
;②![]() ,详见解析;(3)
,详见解析;(3)![]() 或
或![]()
【解析】
(1)[思维教练]由![]() 和
和![]() 均为等边三角形可证
均为等边三角形可证![]() ,即可知AD与BE之间的数量关系,再由等边三角形和全等三角形的性质求得
,即可知AD与BE之间的数量关系,再由等边三角形和全等三角形的性质求得![]() 的度数;
的度数;
[自主作答]
(2)[思维教练]由![]() 和
和![]() 均为等腰直角三角形可证
均为等腰直角三角形可证![]() ,即可知
,即可知![]() ,
,![]() ,再由
,再由![]() 是等腰直角三角形,可知
是等腰直角三角形,可知![]() ,从而证明结论.
,从而证明结论.
[自主作答]
(3)[思维教练]根据题意可作以点D为圆心,PD长为半径的圆,再过点B作圆的切线,分两种情况:第一种情况过点A作![]() 于点M,过点A作AP的垂线,交BP于点
于点M,过点A作AP的垂线,交BP于点![]() ,易证
,易证![]() ,即可得
,即可得![]() ,由勾股定理可求PB的长,从而求得
,由勾股定理可求PB的长,从而求得![]() 的长,再由
的长,再由![]() 是等腰直角三角形可得
是等腰直角三角形可得![]() ,即可求解;第二种情况与第一种情况相同解法可得
,即可求解;第二种情况与第一种情况相同解法可得![]() ,运用勾股定理和全等三角形求出
,运用勾股定理和全等三角形求出![]() 与PB的长即可求解.
与PB的长即可求解.
解:(1)① 60°;②![]() ;
;
[解法提示]①![]() 和
和![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;②由①得
;②由①得![]() ,
,![]() .
.
(2)①![]() ;②
;②![]() .理由如下:
.理由如下:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .在等腰直角三角形
.在等腰直角三角形![]() 中,
中,![]() 为斜边
为斜边![]() 上的高,
上的高,![]() ,
,![]() ,
,![]() ;
;
(3) ![]() 或
或![]() .
.
[解法提示]![]() ,
,![]() ,
,![]() 是以点
是以点![]() 为圆心,以1为半径的
为圆心,以1为半径的![]() 的切线,点
的切线,点![]() 为切点.第一种情况:如解图①,过
为切点.第一种情况:如解图①,过![]() 点作
点作![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,第二种情况:如解图②,可得
,第二种情况:如解图②,可得![]() .
.
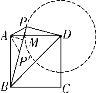
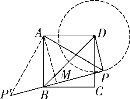
图① 图②


科目:初中数学 来源: 题型:
【题目】为美化小区,物业公司计划对面积为![]() 的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队的
的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队的![]() 倍,如果要独立完成面积为
倍,如果要独立完成面积为![]() 区域的绿化,甲队比乙队少用
区域的绿化,甲队比乙队少用![]() 天.
天.
![]() 求甲、乙两工程队每天能完成绿化的面积分别是多少
求甲、乙两工程队每天能完成绿化的面积分别是多少![]() ?
?
![]() 若物业公司每天需付给甲队的绿化费用为
若物业公司每天需付给甲队的绿化费用为![]() 万元,需付给乙队的费用为
万元,需付给乙队的费用为![]() 万元,要使这次的绿化总费用不超过
万元,要使这次的绿化总费用不超过![]() 万元,至少应安排甲队工作多少天?
万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
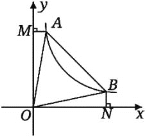
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A、B两点,连接OA、OB,
交于A、B两点,连接OA、OB,![]() 轴于点M,
轴于点M,![]() 轴于点N,有以下结论:①
轴于点N,有以下结论:①![]() ;②
;②![]() ;③
;③![]() 则
则![]() ;④当
;④当![]() 时,
时,![]() .其中结论正确的是___________
.其中结论正确的是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为l的方格纸中,有线段AB,BC.点A,B,C均在小正方形的顶点上.
(1)在图1中画出四边形ABCD,四边形ABCD是轴对称图形,点D在小正方形的项点上:
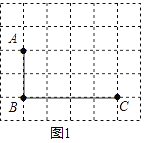
(2)在图2中画四边形ABCE,四边形ABCE不是轴对称图形,点E在小正方形的项点上,∠AEC=90°,EC>EA;直接写出四边形ABCE的面积为________.
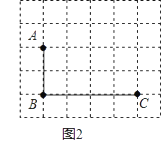
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=![]() BC,③OD=
BC,③OD=![]() BF,④∠CHF=45°。正确结论的个数为( )
BF,④∠CHF=45°。正确结论的个数为( )
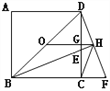
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8,点E是AB的中点,以AE为边作等边△ADE(点D与点C分别在AB异侧),连接CD,则△ACD的面积是_________.
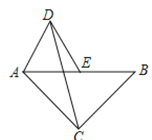
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩(x)分为四个等级:优秀![]() ;良好
;良好![]() ;及格
;及格![]() ;不及格
;不及格![]() ,并绘制成以下两幅统计图.
,并绘制成以下两幅统计图.
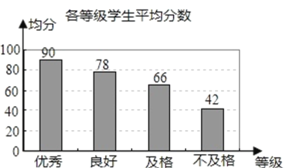

根据以上信息,解答下列问题:
(1)在抽取的学生中不及格人数所占的百分比是______;
(2)计算所抽取学生测试成绩的平均分;
(3)若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com