
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
如图①,△ABC的角平分线BD、CE相交于点P.
(1)如果∠A=70°,求∠BPC的度数;
(2)如图②,过P点作直线MN∥BC,分别交AB和AC于点M和N,试求
∠MPB+∠NPC的度数(用含∠A的代数式表示);
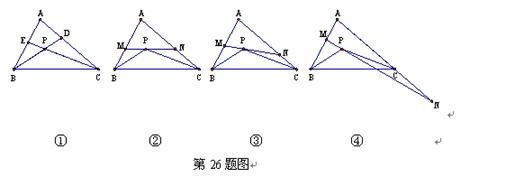
(3)在(2)的条件下,将直线MN绕点P旋转.
(i)当直线MN与AB、AC的交点仍分别在线段AB和AC上时,如图③,
试 探索∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由;
探索∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由;
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的
延长线上时,如图④,试问(i)中∠MPB、∠NPC、∠A三者之间
的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请
给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了了解我市10000名学生参加初中毕业考试数学成绩情况,从中抽取了500名考生的成绩进行统计.在这个问题中,下列 说法: ①这10000名学生的数学考试成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.
说法: ①这10000名学生的数学考试成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.
其中说法正确的有
A. 4个 B. 3个 C. 2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
在 △ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,
△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,
CD 平分∠ECA.
平分∠ECA.
(1) 求证:四边形ABCD是菱形.
(2 ) 若AB=2,连接BD,求BD长。
) 若AB=2,连接BD,求BD长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【操作发现】如图,现有1×1,1×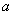 ,1×
,1×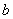 ,
,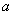 ×
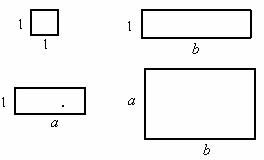
×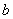 的矩形卡片各一张,请你在下面的方框内将它们拼成一个大的矩形(要求:画出分割线,并标注必要的线段长)。观察操作前
的矩形卡片各一张,请你在下面的方框内将它们拼成一个大的矩形(要求:画出分割线,并标注必要的线段长)。观察操作前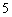 后的面积可以得到一个等式,这个等式是__________________________。
后的面积可以得到一个等式,这个等式是__________________________。

【应用探 究】对于一个正整数n,若能找到正整数
究】对于一个正整数n,若能找到正整数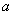 ,
,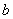 ,使得n=
,使得n=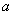 +
+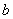 +
+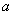
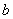 ,则称n为一个“妙数”。例如3=1+1+1×1,则3就是一个“妙数”。根据“妙数”的规定,解决下列问题:
,则称n为一个“妙数”。例如3=1+1+1×1,则3就是一个“妙数”。根据“妙数”的规定,解决下列问题:
5是不是一个 “妙数”?为什么?
从1到10这10个正整数中“妙数”有________个.
【活动拓展】在一次数学活动课上,黑板上写有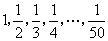 共50个数字。李老师要求同学们进行以下操作:每次操作先从黑板上的数中任选取2个数
共50个数字。李老师要求同学们进行以下操作:每次操作先从黑板上的数中任选取2个数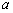 、
、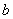 ,然后删去这两个数
,然后删去这两个数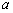 和
和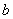 ,同时在黑板上写出与
,同时在黑板上写出与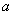 +
+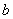 +
+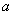

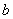 的值相等的数.试求经过49次操作后黑板上剩
的值相等的数.试求经过49次操作后黑板上剩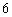 下的数.
下的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com