
【题目】将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,点E,F分别在边
,点E,F分别在边![]() ,
,![]() 上.沿着
上.沿着![]() 折叠该纸片,使得点A落在
折叠该纸片,使得点A落在![]() 边上,对应点为
边上,对应点为![]() ,如图①.再沿
,如图①.再沿![]() 折叠,这时点E恰好与点C重合,如图②.
折叠,这时点E恰好与点C重合,如图②.

(Ⅰ)求点C的坐标;
(Ⅱ)将该矩形纸片展开,再折叠该矩形纸片,使点O与点F重合,折痕与![]() 相交于点P,展开矩形纸片,如图③.
相交于点P,展开矩形纸片,如图③.
①求![]() 的大小;
的大小;
②点M,N分别为![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,求点N的坐标(直接写出结果即可).
取得最小值时,求点N的坐标(直接写出结果即可).
【答案】(Ⅰ)![]() (Ⅱ)①
(Ⅱ)①![]() ,②
,②![]()
【解析】
(Ⅰ)由翻折的性质可知,![]() ,
,![]() ,再由正方形的性质和勾股定理可得OE,继而即可求解;
,再由正方形的性质和勾股定理可得OE,继而即可求解;
(Ⅱ)①连接![]() ,由题意和(Ⅰ)可知,而
,由题意和(Ⅰ)可知,而![]() ,
,![]() ,由等角对等边可知
,由等角对等边可知![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,然后根据翻折的性质可知
,然后根据翻折的性质可知![]() 即
即![]() ,把x代入列出方程,解方程求出
,把x代入列出方程,解方程求出![]() ,根据相似三角形的判定可证,
,根据相似三角形的判定可证, ![]() ,再根据相似三角形的对应角相等和三角形内角和即可求解;
,再根据相似三角形的对应角相等和三角形内角和即可求解;
②利用角平分线上的点到角两边的距离相等这一性质可判断M、N的位置,进而根据题意即可求解.
解:(Ⅰ)∵点![]() ,∴
,∴![]() .
.
由两次折叠可知,![]() ,
,![]() .
.
∴![]() 是正方形.∴
是正方形.∴![]() .
.
在![]() 中,
中,![]() .
.
∴点C的坐标为![]() .
.
(Ⅱ)①如图③,连接![]() ,由
,由![]() 和(Ⅰ)可知,
和(Ⅰ)可知,
![]() ,而
,而![]() ,
,
![]() ,
,
故![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,
由![]() 即
即![]() ,
,
得![]() ,解得
,解得![]() .
.
所以![]() .则有
.则有![]() .
.
得![]() .又
.又![]() ,则
,则![]() ,
,
即![]() .
.
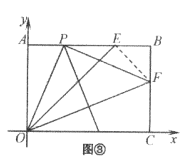
②如图④所示,过点P作![]() ⊥OC于点
⊥OC于点![]() ,交OF于点M,作
,交OF于点M,作![]() 关于OF的对称点N,连接MN,此时
关于OF的对称点N,连接MN,此时![]() 取得最小值时,且
取得最小值时,且![]() ,
,
过点N作NG⊥x轴于点G,
∵由(Ⅱ)知,∠AOE=45°,
∴∠NOG=90°-45°=45°
∴OG=NG=![]() .
.
∴![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
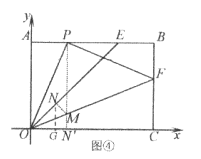
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
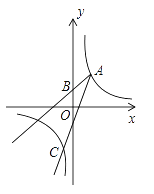
【题目】如图1,在四边形ABCD内接于⊙O,AB=AC,BD为⊙O的直径,AE⊥BD,垂足为点E,交BC于点F.
(1)求证:FA=FB;
(2)如图2,分别延长AD,BC交于点G,点H为FG的中点,连接DH,若tan∠ACB=![]() ,求证:DH为⊙O的切线;
,求证:DH为⊙O的切线;
(3)在(2)的条件下,若DA=3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,物质生活极大丰富,青少年的营养过剩,身体越来越胖,某校为了了解八年级学生的体重情况,随机抽取了八年级部分学生进行调查,将抽取学生的体重情况绘制成如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
组别 | 体重(千克} | 人数 |
A |
| 3 |
B |
| 12 |
C |
| a |
D |
| 10 |
E |
| 8 |
F |
| 2 |
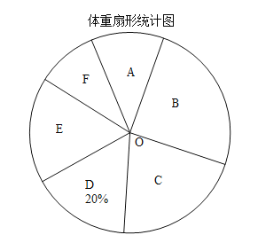
(1)求得![]() __________(直接写出结果); 在扇形统计图中,D组所在扇形的圆心角的度数等于_________ ;
__________(直接写出结果); 在扇形统计图中,D组所在扇形的圆心角的度数等于_________ ;
(2)调查的这组数据的中位数落在_________组;
(3)如果体重不低于55千克,属于偏胖,该校八年级有1200名学生,请估算该年级体重偏胖的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2/span>D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
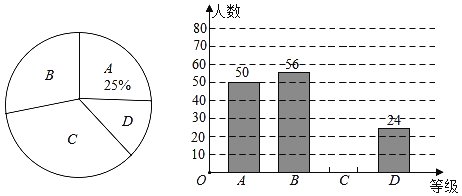
【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.我市某中学举办了网上诗词大赛,大赛的成绩分为四个等级:优秀、良好、及格、不及格(分别用A,B,C,D表示).为了了解该校学生对诗词的掌握程度,赛后随机抽取了部分学生的成绩进行整理,并将结果绘制了如下两幅不完整的统计图.
(1)本次抽取的学生共有 人,扇形统计图中不及格学生所占的圆心角的度数为 .
(2)请根据计算补全条形统计图;
(3)若某校有1200名学生,请你根据调查结果估计该校学生诗词大赛成绩为“优秀”和“良好”两个等级共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com