
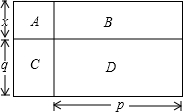
 如图,大长方形是由1个小正方形(A)和3个小长方形(B、C、D)拼成的,请根据图中数据解决下列问题:
如图,大长方形是由1个小正方形(A)和3个小长方形(B、C、D)拼成的,请根据图中数据解决下列问题:

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
 (2012•六合区一模)观察猜想
(2012•六合区一模)观察猜想查看答案和解析>>
科目:初中数学 来源:2012届江苏省南京市六合区中考一模数学试卷(带解析) 题型:解答题
观察猜想
如图,大长方形是由四个小长方形拼成的,请根据此图填空: =
= = ( )( ).
= ( )( ).
说理验证
事实上,我们也可以用如下方法进行变形: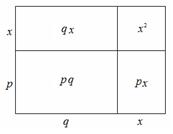
 =
= =
=
= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把 分解因式.
分解因式.
解: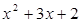 =
= =
= .
.
请利用上述方法将下列多项式分解因式:
【小题1】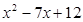 ;
;
【小题2】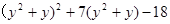 .
.
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-因式分解的应用(解析版) 题型:解答题
如图,大长方形是由四个小长方形拼成的,请根据此图填空:x2+(p+q)x+pq=x2+px+qx+pq=( )( ).
说理验证
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+()= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把x2+3x+2分解因式.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式分解因式:
(1)x2﹣7x+12; (2)(y2+y)2+7(y2+y)﹣18.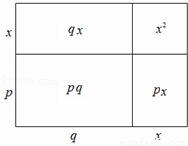
查看答案和解析>>
科目:初中数学 来源:2012年江苏省南京市六合区中考一模数学试卷(解析版) 题型:解答题
观察猜想
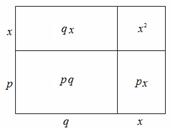
如图,大长方形是由四个小长方形拼成的,请根据此图填空:
 =
=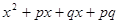 =
( )( ).
=
( )( ).
说理验证
事实上,我们也可以用如下方法进行变形:
 =
=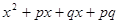 =
=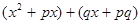
= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把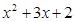 分解因式.
分解因式.
解: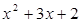 =
= =
= .
.
请利用上述方法将下列多项式分解因式:
1.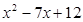 ;
;
2.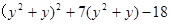 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com