Question

20．如图1，抛物线y=-x²+bx+c与x轴交于A、B两点（点A在点B左侧），与y轴交于C点，CD∥x轴交该抛物线于点D，点A、D的坐标分别为（-1，0），（3，4），点E在x轴上，且tan∠DEA=$\frac{4}{3}$．
（1）求抛物线的解析式和点E的坐标；
（2）如图2，点P从点O出发以每秒1个单位长度的速度沿O→E匀速运动，过点P作直线l∥DE，当点P运动时，直线l也随之运动，设四边形OCDE被直线l扫过的面积为S，求S与t之间的函数解析式；
（3）如图3，当（2）中的点P从点O出发以每秒1个单位长度的速度沿O→E匀速运动时，另一动点Q从点E出发，以每秒2个单位长度的速度沿E→D→C→O匀速运动，当点P到达终点E时，点Q也随之停止运动，若点P、Q同时出发，运动时间为t秒，则t为何值时，以D、P、Q为顶点的三角形是直角三角形？请直接写出所有符合条件的t值．

Answer 1

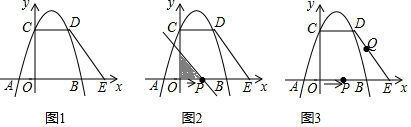
分析 （1）用待定系数法求出抛物线解析式，用锐角三角函数求出EF，进而得出点E坐标；
（2）分两种情况讨论计算，①扫过部分是三角形，直接用三角形的面积公式计算即可，②扫过部分梯形用梯形的面积减去平行四边形的面积；
（3）分点Q在DE，CD，OC上分别进行计算，点Q在CD上时，有两种情况．

解答 解：（1）如图1，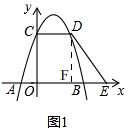

点A（-1，0），D（3，4）在抛物线y=-x²+bx+c上，
∴$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=4}\end{array}\right.$，
∴$\left\{\begin{array}{l}{b=3}\\{c=4}\end{array}\right.$，
∴抛物线y=-x²+3x+4，
∴C（0，4），
∵CD∥x轴，
∴D（3，4），
过点D作DF⊥x轴，
∵tan∠DEA=$\frac{4}{3}$．
∴$\frac{DF}{EF}$=$\frac{4}{3}$，
∵DF=4，
∴EF=3，
∴E（6，0）．
（2）如图2，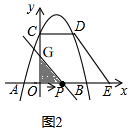
当0＜t≤3时，由（1）知，点D（3，3），E（6，0），
∴直线DE解析式为y=-$\frac{4}{3}$x+8，
∵直线l∥DE，而P（t，0），
∴直线l解析式为y=-x+$\frac{4}{3}$t，
∴G（0，$\frac{4}{3}$t）；
∴OP=t，OG=$\frac{4}{3}$t，
∴S=$\frac{1}{2}$OP×OG=$\frac{1}{2}$t×$\frac{4}{3}$t=$\frac{2}{3}{t}^{2}$，
当3＜t＜6时，如图3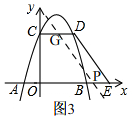，OP=t，CD=3，OE=6，OC=4，
∴PE=6-t
∴S=S_梯形CDEO-S_{平行四边形PEDG}=$\frac{1}{2}$（CD+OE）•OC-PE•OC=$\frac{1}{2}$（3+6）×4-（6-t）×4=4t-6；
（3）如图4，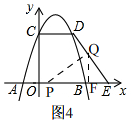
①当点Q在DE上时，（0＜t＜$\frac{5}{2}$），即：∠PQD=90°，
∴PQ⊥DE，
由（2）知，直线DE解析式为y=-$\frac{4}{3}$x+8，
∵P（t，0），
∴PQ的解析式为y=$\frac{3}{4}$x-$\frac{3}{4}$t，
∵Q（6-$\frac{6}{5}$t，$\frac{8}{5}$t），
∴$\frac{3}{4}$（6-$\frac{6}{5}$t）-$\frac{3}{4}$t=$\frac{8}{5}$t，
∴t=$\frac{18}{13}$，
②当点Q在CD上时，（$\frac{5}{2}$≤t≤4），
Ⅰ、当∠DQP=90°，
∴x_P=x_Q，
∵P（t，0），Q（8-2t，4），
∴8-2t=t，
∴t=$\frac{8}{3}$，
Ⅱ、当∠PDQ=90°，
∴x_P=x_D，
∴t=3，
③如图5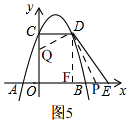，当Q在OC上时，（4＜t＜6），
∴∠QDP=90°，过点D作DF⊥AE，
∴∠CDF=90°，
∴∠CDQ=∠PDF，
在Rt△CDQ中，CD=3，CQ=2t-8，
∴tan∠CDQ=$\frac{CQ}{CD}=\frac{12-2t}{3}$$\frac{CQ}{CD}=\frac{2t-8}{3}$，
在Rt△PDF中，PF=t-3，DF=4，
∴tan∠PDF=$\frac{PF}{DF}=\frac{t-3}{4}$，
∴$\frac{2t-8}{3}=\frac{t-3}{4}$，
∴t=$\frac{23}{5}$
即：满足条件的t的值为，$\frac{18}{13}$，$\frac{8}{3}$，3，$\frac{23}{5}$．

点评 此题是二次函数综合题，主要考查了待定系数法，锐角三角函数，三角形，梯形面积公式，解本题的关键是根据运动表示出点Q的坐标，用分类讨论的思想解决问题，注意不要漏解，是一道比较好的中考常考题．