
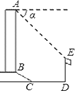
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为________米.(精确到0.1米,参考数据:
,则大楼AB的高度为________米.(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】6![]() +29
+29
【解析】
延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=![]() x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6
x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6![]() 米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6
米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6![]() +20(米),即可得出大楼AB的高度.
+20(米),即可得出大楼AB的高度.
延长AB交DC于H,作EG⊥AB于G,如图所示:
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:![]() ,
,
∴BH:CH=1:![]() ,
,
设BH=x米,则CH=![]() x米,
x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+(![]() x)2=122,
x)2=122,
解得:x=6,
∴BH=6米,CH=6![]() 米,
米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=6![]() +20(米),
+20(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6![]() +20(米),
+20(米),
∴AB=AG+BG=6![]() +20+9=(6
+20+9=(6![]() +29)m.
+29)m.
故答案为:6![]() +29.
+29.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,用树状图表示或列表法求足球踢到了小华处的概率是多少
(2)如果从小明开始踢,经过踢三次后,球踢到了小明处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
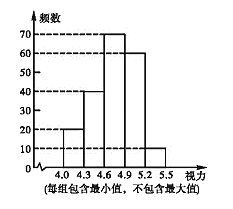
【题目】建华区对参加![]() 年中考的
年中考的![]() 名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图、表信息解答下列问题:
名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图、表信息解答下列问题:
(1)在频数分布表中,![]() 的值为 ,
的值为 ,![]() 的值为 ,并将频数分布直方图补充完整;
的值为 ,并将频数分布直方图补充完整;
(2)甲同学说:“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围?
(3)若视力在![]() 以上(含
以上(含![]() )均属正常,则视力正常的人数占被统计人数的百分比是 ,并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
)均属正常,则视力正常的人数占被统计人数的百分比是 ,并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
视力 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“守护碧水蓝天,守护我们的家园”,某市为了改善城市环境,预算 116 万元购进 A、B 两种型号的清扫机,已知 A 型号清扫机的单价比 B 型号清扫 机单价的 ![]() 多 1.2 万元,若购进 2 台 A 型号清扫机和 3 台 B 型号清扫机花费 54.6 万元.
多 1.2 万元,若购进 2 台 A 型号清扫机和 3 台 B 型号清扫机花费 54.6 万元.
(1)求 A 型号清扫机和 B 型号清扫机的单价分别为多少万元;
(2)该市通过考察决定先购进两种型号的清扫机共 10 台,且 B 型号的清扫机 数量不能少于 A 型号清扫机的 1.5 倍,该市怎样购买才能花费最少?最少花费 多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
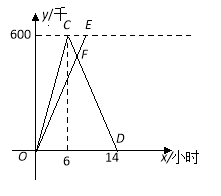
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距100千米时,求甲车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抗击新冠病毒疫情,全国人民众志成城,守望相助.春节后某地一水果购销商安排15辆汽车装运A,B,C三种水果120吨销售,所得利润全部捐赠湖北抗疫.已知按计划15辆汽车都要装满且每辆汽车只能装同一种水果,每种水果所用车辆均不少于3辆,汽车对不同水果的运载量和每吨水果销售获利情况如下表.
水果品种 | A | B | C |
汽车运载量(吨/辆) | 10 | 8 | 6 |
水果获利(元/吨) | 800 | 1200 | 1000 |
(1)设装运A种水果的车辆数为x辆,装运B种水果车辆数为y辆,根据上表提供的信
息,
①求y与x之间的函数关系式;
②设计车辆的安排方案,并写出每种安排方案;
(2)若原有获利不变的情况下,当地政府按每吨50元的标准实行运费补贴,该经销商打算将获利连同补贴全部捐出.问应采用哪种车辆安排方案,可以使这次捐款数w(元)最大化?捐款w(元)最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
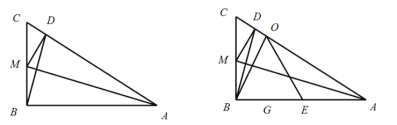
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
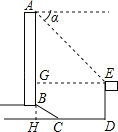
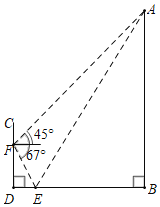
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上(如图所示).该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为45°,平面镜E的俯角为67°,测得FD=2.4米.求旗杆AB的高度约为多少米?(结果保留整数,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意的实数m,n,定义运算“∧”,有m∧n=![]() .
.
(1)计算:3∧(-1);
(2)若![]() ,
,![]() ,求m∧n (用含x的式子表示);
,求m∧n (用含x的式子表示);
(3)若![]() ,
,![]() , m∧n=-2 ,求x的值 .
, m∧n=-2 ,求x的值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com