
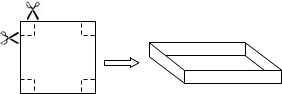
 如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.
如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2. 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值 】
】 =-
=-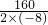 =10时,S最大值=
=10时,S最大值=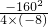 =800.
=800.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
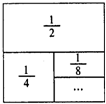 如图,在一个边长为1的正方形纸板上,依次贴上面积为
如图,在一个边长为1的正方形纸板上,依次贴上面积为| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
查看答案和解析>>
科目:初中数学 来源: 题型:
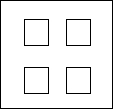 如图,在一个边长为acm的正方形木板上,挖掉四个边长为bcm(b<
如图,在一个边长为acm的正方形木板上,挖掉四个边长为bcm(b<| a | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
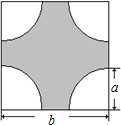 如图,在一个边长为b厘米的正方形铁板的四角,各剪去一个半径为a厘米(a≤
如图,在一个边长为b厘米的正方形铁板的四角,各剪去一个半径为a厘米(a≤| b |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为
我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com