Question

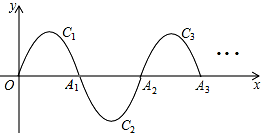
9．如图，一条抛物线y=-x（x-2）（0≤x≤2）的一部分，记为C₁，它与x轴交于O，A₁两点，将C₁绕点A₁旋转180°得到C₂，交x轴于点A₂，；将C₂绕点A₂旋转180°得到C₃，交x轴于A₃；…如此进行下去，直至得到C₆，若点P（2017，y）在抛物线C_n上，则y=1．

Answer 1

分析 根据抛物线与x轴的交点问题，得到图象C₁与x轴交点坐标为：（0，0），（2，0），再利用旋转的性质得到图象C₂与x轴交点坐标为：（2，0），（4，0），则抛物线C₂：y=（x-2）（x-4）（2≤x≤4），于是可推出横坐标x为偶数时，纵坐标为0，横坐标是奇数时，纵坐标为1或-1，只要判断n的值即可解决问题．

解答 解：∵一段抛物线C₁：y=-x（x-2）（0≤x≤2），
∴图象C₁与x轴交点坐标为：（0，0），（2，0），
∵将C₁绕点A₁旋转180°得C₂，交x轴于点A₂；，
∴抛物线C₂：y=（x-2）（x-4）（2≤x≤4），
将C₂绕点A₂旋转180°得C₃，交x轴于点A₃；
…
∴P（2017，y）在抛物线C₁₀₀₉上，
∵n=1009是奇数，
∴P（2017，y）在x轴的上方，y=1，
∴当x=2017时，y=1．
故答案为1．

点评 本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．