
【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE. 
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
【答案】
(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠A=∠AEB
(2)证明:∵DC⊥OE,
∴DF=CF,
∴OE是CD的垂直平分线,
∴ED=EC,又DE=DC,
∴△DEC为等边三角形,
∴∠AEB=60°,又∠A=∠AEB,
∴△ABE是等边三角形.
【解析】(1)根据圆内接四边形的性质得到∠A=∠DCE,根据等腰三角形的性质得到∠DCE=∠DEC,等量代换证明结论;(2)根据垂径定理得到OE是CD的垂直平分线,根据题意证明△DEC为等边三角形,证明结论.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆内接四边形的性质的理解,了解把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,直角坐标系中有一矩形OABC,其中O是坐标原点,点A,C分别在x轴和y轴上,点B的坐标为(3,4),直线y= ![]() x交AB于点D,点P是直线y=
x交AB于点D,点P是直线y= ![]() x位于第一象限上的一点,连接PA,以PA为半径作⊙P,
x位于第一象限上的一点,连接PA,以PA为半径作⊙P, 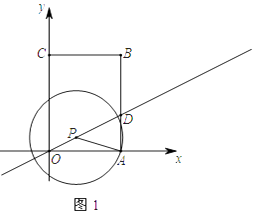
(1)连接AC,当点P落在AC上时,求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m, ①在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
②如图2,记⊙P与直线y= ![]() x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足
x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足 ![]() <
< ![]() <3时,求m的取值范围.(请直接写出答案)
<3时,求m的取值范围.(请直接写出答案)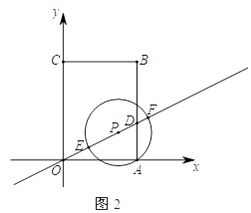
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB. 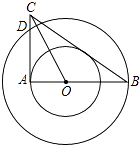
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2![]() =2+2
=2+2![]() +1=(
+1=(![]() )2+2
)2+2![]() +1=(
+1=(![]() +1)2;
+1)2;
5+2![]() =2+2
=2+2![]() +3=(
+3=(![]() )2+2×
)2+2×![]() ×
×![]() +(
+(![]() )2=(
)2=(![]() +
+![]() )2
)2
(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2![]() ;②6+4
;②6+4![]()
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分): 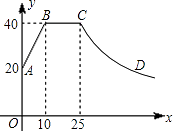
(1)上课后第5min与第30min相比较,何时学生注意力更集中?
(2)某道难题需连续讲19min,为保证效果,学生注意力指数不宜低于36,老师能否在所需要求下讲完这道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E. 
(1)求证:CE是半圆的切线;
(2)若OB=5,BC=8,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下: 
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共吨;
(3)调查发现,在可回收物中塑料类垃圾占 ![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题: 
(1)该镇本次统计的小微企业总个数是 , 扇形统计图中B类所对应扇形圆心角的度数为度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们定义:如果一个数的平方等于﹣1,记作i2=﹣1,那么这个i就叫做虚数单位.虚数与我们学过的实数合在一起叫做复数.一个复数可以表示为a+bi(a,b均为实数)的形式,其中a叫做它的实部,b叫做它的虚部.
复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似.
例如 计算:(5+i)+(3﹣4i)=(5+3)+(i﹣4i)=8﹣3i.
根据上述材料,解决下列问题:
(1)填空:i3= ,i4= ;
(2)计算:(2+i)2;
(3)将![]() 化为a+bi(a,b均为实数)的形式(即化为分母中不含i的形式).
化为a+bi(a,b均为实数)的形式(即化为分母中不含i的形式).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com