
���� ��1������һ�κ�������ʽ���A��B���꣬������κ�������ʽ����������κ�������ʽ��
��2�������������������ߣ�����S=S����OPMB-+S��APM-S��OAC�ɵú�������ʽ��
��3�����ɣ�2���к�����ϵʽ�ó�m��S��ֵ�����ݵ�D���߶�OP���е�ó�D�����꣬���ô���ϵ�������ֱ��AC��BD�Ľ���ʽ���ʿɵó�G�����꣬���������ľ��빫ʽ���DG�ij�������D��DF��AC�ڵ�F�����ֱ��DF�Ľ���ʽ���ʿɵó�F������꣬���DF�ij�������������Ǻ����Ķ��弴�ɵó����ۣ�
��� �⣺��1����y=-$\frac{3}{4}$x+3�У�
��y=0ʱ��x=4������A��4��0����
��x=0ʱ��y=3������B��0��3����
��������y=-$\frac{3}{8}$x2+bx+c����A��B��
��$\left\{\begin{array}{l}-6+4b+c=0\\ c=3\end{array}\right.$�����$\left\{\begin{array}{l}b=\frac{3}{4}\\ c=3\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-$\frac{3}{8}$x2+$\frac{3}{4}$x+3��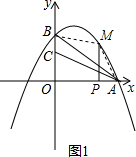
��2����ͼ1��ʾ��
��P��m��0����
��OP=m��PM=-$\frac{3}{8}$m2+$\frac{3}{4}$m+3
��S=S����OPMB+S��APM-S��OAC
=$\frac{1}{2}$��PM+OB��•OP+$\frac{1}{2}$AP•PM-$\frac{1}{2}$OA•OC
=$\frac{1}{2}$��-$\frac{3}{8}$m2+$\frac{3}{4}$m+3+3��•m+$\frac{1}{2}$��4-m����-$\frac{3}{8}$m2+$\frac{3}{4}$m+3��-$\frac{1}{2}$��4��2
=-$\frac{3}{4}$m2+3m+2��0��m��4����
��3�����ɣ�2��֪S=-$\frac{3}{4}$m2+3m+2��
�൱m=2ʱ��S���=5��
��P��2��0����
�ߵ�D���߶�OP���е㣬
��D��1��0����
��ֱ��AC�Ľ���ʽΪy=kx+b��k��0����
��A��4��0����C��0��2����
��$\left\{\begin{array}{l}0=4k+b\\ b=2\end{array}\right.$�����$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=2\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��ֱ��BD�Ľ���ʽΪy=ax+c��a��0����
��B��0��3����D��1��0����
��$\left\{\begin{array}{l}c=3\\ a+c=0\end{array}\right.$�����$\left\{\begin{array}{l}a=-3\\ c=3\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪy=-3x+3��
��$\left\{\begin{array}{l}y=-\frac{1}{2}x+2\\ y=-3x+3\end{array}\right.$�����$\left\{\begin{array}{l}x=\frac{2}{5}\\ y=\frac{9}{5}\end{array}\right.$��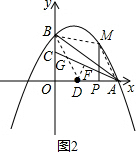
��G��$\frac{2}{5}$��$\frac{9}{5}$����
��DG=$\sqrt{��1-\frac{2}{5}��^{2}+��\frac{9}{5}��^{2}}$=$\sqrt{\frac{9}{25}+\frac{81}{25}}$=$\frac{3\sqrt{10}}{5}$��
����D��DF��AC�ڵ�F��
��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
����ֱ��DF�Ľ���ʽΪy=2x+d��
��D��1��0����
��2+d=0�����d=-2��
����ֱ��DF�Ľ���ʽΪy=2x-2��
��$\left\{\begin{array}{l}y=-\frac{1}{2}x+2\\ y=2x-2\end{array}\right.$�����$\left\{\begin{array}{l}x=\frac{8}{5}\\ y=\frac{6}{5}\end{array}\right.$��
��F��$\frac{8}{5}$��$\frac{6}{5}$����
��DF=$\sqrt{��1-\frac{8}{5}��^{2}+��\frac{6}{5}��^{2}}$=$\frac{3\sqrt{5}}{5}$��
��sin��DGF=$\frac{DF}{DG}$=$\frac{\frac{3\sqrt{5}}{5}}{\frac{3\sqrt{10}}{5}}$=$\frac{\sqrt{2}}{2}$��
���DGF=45�㣬��ֱ��BD��AC���ɵ������45�㣮
���� ���⿼���˶��κ����ۺ��⣬�漰����ϵ������������ʽ�������������ʽ������ͼ���ϵ������������֪ʶ���ۺ���ǿ��ֵ�ù�ע��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ���ı���ABCD�У���֪AB=4��AC=3��BC=5����BC���ڵ�ֱ��Ϊy�ᣬ�Ե�CΪԭ�㽨��ƽ��ֱ������ϵ��x�ύAD�ڵ�E����һ����P��5����λ/����ٶ���A�����������B�㣬�ٵ�C��ֹͣ����һ����F��3����λ/����ٶȴ�C�������x����������˶����͵�Pͬʱ��ʼ��ͬʱֹͣ�˶������˶���ʱ��Ϊt��
��ͼ����ƽ���ı���ABCD�У���֪AB=4��AC=3��BC=5����BC���ڵ�ֱ��Ϊy�ᣬ�Ե�CΪԭ�㽨��ƽ��ֱ������ϵ��x�ύAD�ڵ�E����һ����P��5����λ/����ٶ���A�����������B�㣬�ٵ�C��ֹͣ����һ����F��3����λ/����ٶȴ�C�������x����������˶����͵�Pͬʱ��ʼ��ͬʱֹͣ�˶������˶���ʱ��Ϊt���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
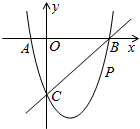 ��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ����࣬B�������Ϊ��4��0������y�ύ��C��0��-4���㣬��P��ֱ��BC�·�����������һ���㣮
��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ����࣬B�������Ϊ��4��0������y�ύ��C��0��-4���㣬��P��ֱ��BC�·�����������һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
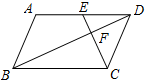 ��ͼ��ƽ���ı���ABCD�У���E��AD����һ�㣬�� CE��BD�ڵ�F������DEC�ش�D��A�ķ���ƽ�ƣ�ʹ��D���A�غϣ���Eƽ�ƺ�ĵ��ΪG��
��ͼ��ƽ���ı���ABCD�У���E��AD����һ�㣬�� CE��BD�ڵ�F������DEC�ش�D��A�ķ���ƽ�ƣ�ʹ��D���A�غϣ���Eƽ�ƺ�ĵ��ΪG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��$\frac{3}{4}$ | B�� | 11��$\frac{3}{4}$ | C�� | 11��-$\frac{3}{4}$ | D�� | 5��-$\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com