
【题目】如图,已知点C、D在线段AB上,且AC=4,BD=9,△PCD是边长为6的等边三角形.
(1)求证:△PAC∽△BPD;
(2)求∠APB的度数.
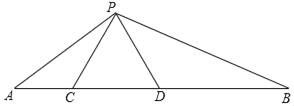
【答案】(1)见解析;(2)120°.
【解析】
试题(1)根据等边三角形的性质得到PC=CD=PD=6,∠PCD=∠PDC=60°,得出∠ACP=∠PDB=120°,由AC=4,BD=9,AC:PD=PC:BD,即可证出△ACP∽△PDB;
(2)由相似三角形的对应角相等,得出∠APC=∠PBD,由三角形内角和定理得出∠DPB+∠DBP=60°,即∠APC+∠BPD=60°,可求出∠APB=120°.
试题解析:(1)∵等边△PCD的边长为6,
∴PC=PD=6,∠PCD=∠PDC=60°,
又∵AC=4,BD=9,
∴![]() ,
,
∵等边△PCD中,∠PCD=∠PDC=60°,
∴∠PCA=∠PDB=120°,
∴△ACP∽△PDB;
(2)∵△ACP∽△PDB,
∴∠APC=∠PBD,
∵∠PDB=120°,
∴∠DPB+∠DBP=60°,
∴∠APC+∠BPD=60°,
∴∠APB=∠CPD+∠APC+∠BPD=120°.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,点A、B、C、D都在格点上.
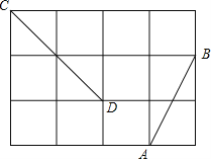
(1)线段AB的长是______;
(2)在图中画出一条线段EF,使EF的长为![]() ,并判断AB、CD、EF三条线段的长能否成为一个直角三角形三边的长?说明理由.
,并判断AB、CD、EF三条线段的长能否成为一个直角三角形三边的长?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
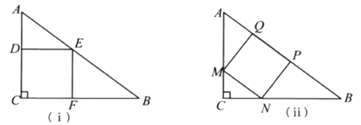
【题目】一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2,请通过计算比较S1与S2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
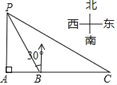
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若∠B=30°,AB=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
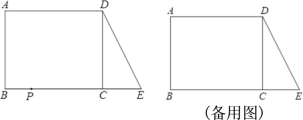
【题目】已知:如图,在长方形ABCD中,AB=DC=4,AD=BC=5.延长BC到E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P运动的时间为t秒.
(1)请用含t的式子表达△ABP的面积S;
(2)是否存在某个t值,使得△DCP和△DCE全等?若存在,请求出所有满足条件的t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
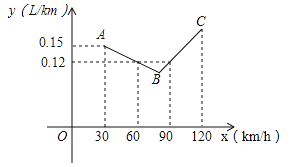
【题目】如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1)当速度为50km/h、100km/h时,该汽车的耗油量分别为 L/km、 L/km.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低.最低是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
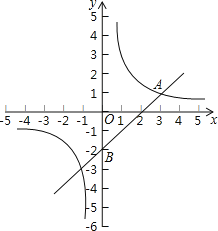
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com