
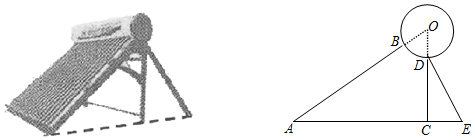
分析 (1)直接利用锐角三角函数关系得出DE=$\frac{DC}{sin∠E}$,进而得出答案;
(2)利用sin∠A=$\frac{CO}{AO}$,得出圆的半径,进而得出答案.
解答 解:(1)在Rt△DCE中,sin∠E=$\frac{CD}{DE}$,
∴DE=$\frac{DC}{sin∠E}$=$\frac{57}{sin60°}$=38$\sqrt{3}$(厘米),
答:辅助支架DE长度38$\sqrt{3}$厘米;
(2)设圆O的半径为x厘米,
在Rt△AOC中,sin∠A=$\frac{CO}{AO}$,
即sin37°=$\frac{57+x}{110+x}$,
∴$\frac{57+x}{110+x}$=$\frac{3}{5}$,
解得:x=22.5≈23(厘米),
答:水箱半径OD的长度为23厘米.
点评 此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:解答题
 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )| A. | 3 | B. | 4.5 | C. | 8-3$\sqrt{3}$ | D. | 8-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
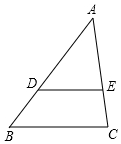 如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.
如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
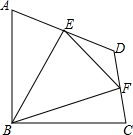 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com