
 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| m+2 |
| 2 |
| 3 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1•x2 |
| m+3 |
| m+2 |
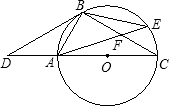
| BF |
| AF |
| 2 |
| 3 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1•x2 |
| m+3 |
| m+2 |
| 2m+1 |
| m2+ m-2 |
| m+3 |
| m+2 |

| BF |
| AF |
| 2 |
| 3 |
| S△BEF |
| S△ACF |
| BF |
| AF |
| 4 |
| 9 |
| b |
| a |
| c |
| a |


科目:初中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.
(2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.查看答案和解析>>
科目:初中数学 来源: 题型:
 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.查看答案和解析>>
科目:初中数学 来源:2012届四川乐山市中区中考模拟数学试卷(带解析) 题型:解答题
选做题:本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
甲题:由山脚下的一点A测得山顶D的仰角是45°,从 沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
 |
 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO= .
.
 y.
y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com