
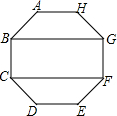
 如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2.
如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2.分析 (1)根据正八边形的性质得出正八边形每个内角相等和多边形内角和定理即可得出结果;
(2)以表示出四边形ABGH面积进而求出答案即可;
(3)由(2)即可得出结果.
解答 解:(1)∵正八边形每个内角相等,
∴∠A=$\frac{1}{8}$(8-2)×180°=135°;
(2)连接HE,AD,如图所示: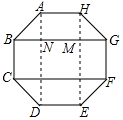
在正八边形ABCDEFGH中,可得:HE⊥BG于点M,AD⊥BG于点N,
∵∠HGM=45°,
∴MH=MG,
∵点A到线段BG的距离是a,
则AN=MH=MG=a,HG=AH=AB=GF=$\sqrt{2}$a,
∴BG×GF=2( $\sqrt{2}$+1)a2=20,
∴a2=$\frac{10}{\sqrt{2}+1}$=10($\sqrt{2}$-1);
(3)由(2)得:四边形ABGH面积=$\frac{1}{2}$(AH+BG)×HM=( $\sqrt{2}$+1)a2=10,
∴正八边形的面积为:10×2+20=40(cm2).
点评 此题主要考查了正八边形的性质以及勾股定理等知识,根据已知得出四边形ABGH面积是解决问题(3)的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
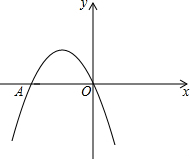 如图,二次函数y=ax2-4x+c的图象经过坐标原点,与x轴交于点A(-4,0).
如图,二次函数y=ax2-4x+c的图象经过坐标原点,与x轴交于点A(-4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com