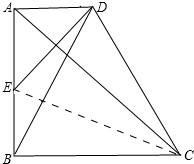
(1)证明:连接CE,
∵AC为线段ED的垂直平分线,
∴AD=AE,DC=EC,∠EAC=∠DAC=45°,
∴三角形ABC为等腰直角三角形,即AB=BC,
∵E为线段AB的中点,
∴AE=EB,即AD=BE,
又∠DAB=∠EBC=90°,
∴△ADB≌△BEC,
∴EC=BD,
∴BD=DC;
(2)解:延长线段CB,在延长线上截取BC′=BC,连接C′D,与AB交于点P,
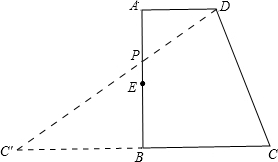
∵E为AB中点,∴AE=EB,又AD=AE=1,∴AB=2,
由(1)得到BD=DC,即三角形DBC为等腰三角形,
过点D作DM⊥BC,垂直为M,则BM=CM=AD=1,
∴BC′=BC=2,
∵AD∥BC,
∴∠ADC′=∠C′,∠DAP=∠C′PB,
∴△APD∽△BPC′,
∴
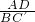
=

,
设PB=x,则AP=2-x,则

=

,
解得:x=

,则PB=

.
分析:(1)连接EC,由AC垂直平分ED,根据中垂线的性质得到AD=AE,DC=EC,所以三角形AED为等腰直角三角形,即∠EAC=∠DAC=45°,进而得到△ABC为等腰直角三角形,所以AB=BC,由E为AB中点得到AE=EB,等量代换得到AD=EB,从而利用“SAS”证明△ADB≌△BEC,得到DB=EC,等量代换得证;
(2)延长线段CB,在延长线上截取BC′=BC,连接C′D,与AB的交点即为所求的点P,然后由(1得到DB=EC,即三角形DBC为等腰三角形,由AD的长求出BC的长,即为C′B的长,再由E为AB中点,AC为ED中垂线,得到AB=2AD=2,由AD∥BC,根据两直线平行,得到两对内错角相等,从而得到△APD∽△BPC′,得到对应边成比例,设PB为x,得到AP=2-x,代入比例式中即可求出PB的长.
点评:此题综合考查了对称的性质,等腰三角形的性质,全等三角形的判定以及相似三角形的判别与性质.学生作第一问时注意等量间的代换,第二问的关键是利用两点之间,线段最短和对称知识找出满足题意的P点.

 (1)证明:连接CE,
(1)证明:连接CE,
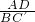 =
= ,
, =
= ,
, ,则PB=
,则PB= .
.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=