
| A. | 南偏东60° | B. | 南偏西30° | C. | 北偏西30° | D. | 南偏西60° |
分析 首先根据速度和时间计算出行驶路程,再根据勾股定理逆定理结合路程可判断出甲和乙两艘轮船的行驶路线呈垂直关系,进而可得答案.
解答 解:如图:
∵甲乙两艘客轮同时离开港口,航行的速度都是每分钟40m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,
∴甲客轮走了40×15=600(m),乙客轮走了40×20=800(m),
∵A、B两点的直线距离为1000m,
∴6002+8002=10002,
∴∠AOB=90°,
∵甲客轮沿着北偏东30°的方向航行,
∴乙客轮的航行方向可能是南偏东60°,
故选:A.
点评 此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
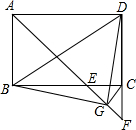 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
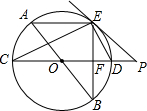 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )| A. | 两点之间,线段最短 | B. | 直角三角形的两个锐角互余 | ||
| C. | 三角形三个内角和等于180° | D. | 三角形具有稳定性 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com