
【题目】传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=![]()
(1)李明第几天生产的粽子数量为280只?
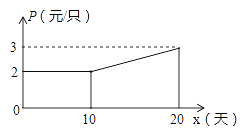
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
【答案】(1)李明第10天生产的粽子数量为280只.(2)第13天的利润最大,最大利润是578元.
【解析】(1)把y=280代入y=20x+80,解方程即可求得;
(2)根据图象求得成本p与x之间的关系,然后根据利润等于订购价减去成本价,然后整理即可得到W与x的关系式,再根据一次函数的增减性和二次函数的增减性解答.
(1)设李明第x天生产的粽子数量为280只,
由题意可知:20x+80=280,
解得x=10.
答:第10天生产的粽子数量为420只.
(2)由图象得,当0≤x<10时,p=2;
当10≤x≤20时,设P=kx+b,
把点(10,2),(20,3)代入得,
![]() ,
,
解得![]() ,
,
∴p=0.1x+1,
①0≤x≤6时,w=(4-2)×34x=68x,当x=6时,w最大=408(元);
②6<x≤10时,w=(4-2)×(20x+80)=40x+160,
∵x是整数,
∴当x=10时,w最大=560(元);
③10<x≤20时,w=(4-0.1x-1)×(20x+80)=-2x2+52x+240,
∵a=-3<0,
∴当x=-![]() =13时,w最大=578(元);
=13时,w最大=578(元);
综上,当x=13时,w有最大值,最大值为578.


科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC
(1)填空:如图1,∠B= °,∠C= °;
(2)如图2,若M为线段BC上的点,过M作MH⊥AD,交AD的延长线于点H,分别交直线AB、AC与点N、E.
①求证:△ANE是等腰三角形;
②线段BN、CE、CD之间的数量关系是 .
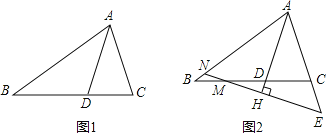
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决后面的问题
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707--1783)才发现指数与对数之间的联系,我们知道,n个相同的因数a相乘aa…,a记为an,如23=8,此时,3叫做以2为底8的对数,记为log28,即log28=3一般地若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab,即logab=n.如34=81,则4叫做以3为底81的对数,记为log381,即log381=4.
(1)计算下列各对数的值:log24=______,log216=______,log264=______;
(2)通过观察(1)中三数log24、log216、log264之间满足的关系式是______;
(3)拓展延伸:下面这个一股性的结论成立吗?我们来证明logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴aman=am+n=MN,
∴logaMN=m+n,
又∵logaM=m,logaN=n,
∴logaM+logaN=logaMN(a>0且a≠1,M>0,N>0);
(4)仿照(3)的证明,你能证明下面的一般性结论吗?logaM-logaN=loga![]() (a>0且a≠1,M>0,N>0)
(a>0且a≠1,M>0,N>0)
(5)计算:log34+log39-log312的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题与它的逆命题都为真命题的是( )
A. 已知非零实数x,如果![]() 为分式,那么它的倒数也是分式。
为分式,那么它的倒数也是分式。
B. 如果x的相反数为7,那么x为-7。
C. 如果一个数能被8整除,那么这个数也能被4整除。
D. 如果两个数的和是偶数,那么它们都是偶数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴分别交于原点
轴分别交于原点![]() 和点
和点![]() ,与对称轴
,与对称轴![]() 交于点
交于点![]() .矩形
.矩形![]() 的边
的边![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,边
,边![]() ,
,![]() 与抛物线分别交于点
与抛物线分别交于点![]() ,
,![]() .当矩形
.当矩形![]() 沿
沿![]() 轴正方向平移,点
轴正方向平移,点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的同侧时,连接
的同侧时,连接![]() ,此时,四边形
,此时,四边形![]() 的面积记为
的面积记为![]() ;点
;点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的两侧时,连接
的两侧时,连接![]() ,
,![]() ,此时五边形
,此时五边形![]() 的面积记为
的面积记为![]() .将点
.将点![]() 与点
与点![]() 重合的位置作为矩形
重合的位置作为矩形![]() 平移的起点,设矩形
平移的起点,设矩形![]() 平移的长度为
平移的长度为![]() .
.
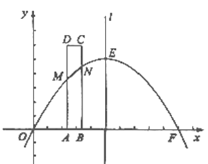
(1)求出这条抛物线的表达式;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当矩形![]() 沿着
沿着![]() 轴的正方向平移时,求
轴的正方向平移时,求![]() 关于
关于![]() 的函数表达式,并求出
的函数表达式,并求出![]() 为何值时,
为何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A、B、C、D均在坐标轴上,AB∥CD.
(1)求证:∠ABO+∠CDO=90°;
(2)如图2,BM平分∠ABO交x轴于点M,DN平分∠CDO交y轴于点N,求∠BMO+∠OND的值.
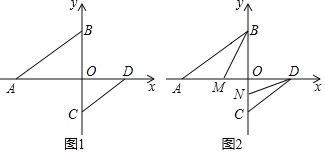
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com