
����Ŀ����ͼ��OABC��ƽ���ı��Σ��Խ���OB��y���������ϣ�λ�ڵ�һ���ĵ�A�͵ڶ����ĵ�C�ֱ���˫����![]() ��
��![]() ��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��![]() ������Ӱ���������
������Ӱ���������![]() ��k1+k2�����۵���AOC=90��ʱ��|k1|=|k2|������OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ����ǣ� ��
��k1+k2�����۵���AOC=90��ʱ��|k1|=|k2|������OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ����ǣ� ��

A���٢ڢ� B���ڢ� C���٢ۢ� D���٢�
���𰸡�D.
��������
�����������AE��y����E��CF��y����F����ͼ��
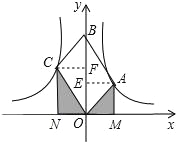
���ı���OABC��ƽ���ı��Σ�
��S��AOB=S��COB��
��AE=CF��
��OM=ON��
��S��AOM=![]() |k1|=
|k1|=![]() OMAM��S��CON=
OMAM��S��CON=![]() |k2|=
|k2|=![]() ONCN��
ONCN��
��![]() ���ʢ���ȷ��
���ʢ���ȷ��
��S��AOM=![]() |k1|��S��CON=
|k1|��S��CON=![]() |k2|��
|k2|��
��S��Ӱ����=S��AOM+S��CON=![]() ��|k1|+|k2|����
��|k1|+|k2|����
��k1��0��k2��0��
��S��Ӱ����=![]() ��k1-k2�����ʢڴ���
��k1-k2�����ʢڴ���
����AOC=90�㣬
���ı���OABC�Ǿ��Σ�
���ȷ��OA��OC��ȣ�
��OM=ON��
����жϡ�AOM�ա�CNO��
����ж�AM=CN��
���ȷ��|k1|=|k2|���ʢ۴���
��OABC��������OA=OC��
��OM=ON��
��Rt��AOM��Rt��CNO��
��AM=CN��
��|k1|=|k2|��
��k1=-k2��
����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ��ʢ���ȷ��
��ѡD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��AB��CD����C�ڵ�D���Ҳ࣬��ABC ����ADC��ƽ���߽��ڵ�E������B��D���غϣ�����ABC��n�㣬��ADC��80��.
��1������B�ڵ�A����࣬����BED�Ķ������ú�n�Ĵ���ʽ��ʾ����
��2������1���е��߶�BC��DC����ƽ�ƣ�����B�ƶ�����A�Ҳ�ʱ���뻭��ͼ�β��ж���BED�Ķ����Ƿ�ı�.���ı䣬�������BED�Ķ������ú�n�Ĵ���ʽ��ʾ���������䣬��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ε���Ǻ͵���360�㣬���������εı���Ϊ�� ��
A. �� B. �� C. �� D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ǽ�����ijһ���������ʱ��仯��ͼ����ͼ��ش�����һ���У�

��1������T�������Dz���ʱ��t��ʱ���ĺ�����
��2��12ʱ�������Ƕ��٣�
��3��ʲôʱ��������ߣ����ʱ���٣�ʲôʱ��������ͣ����ʱ���٣�
��4��ʲôʱ��������������4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�µ�������1.7m������Ӱ�ӳ�Ϊ5.1m��ͬһʱ��ˮ����Ӱ����42m����ˮ���ĸ߶���m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=x2��2x+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0����3����[ͼ2��ͼ3Ϊ�����ͼ]
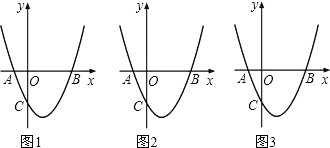
��1��k= ����A������Ϊ ����B������Ϊ ��
��2����������y=x2��2x+k�Ķ���ΪM�����ı���ABMC�������
��3����x���·������������Ƿ����һ��D��ʹ�ı���ABDC�������������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
��4����������y=x2��2x+k�����Q��ʹ��BCQ����BCΪֱ�DZߵ�ֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����OAB��������������ֱ���O��0��0����B��1��1����A��x��y����-2��x��2��-2��y��2��x��y��Ϊ����������������OABΪֱ�������εĸ�����______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ���������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺

��1����A��Ϊ��ת���ģ�����ABC�Ƶ�A˳ʱ����ת90��á�AB1C1��������AB1C1��
��2��������ABC��������ԭ��O�����ĶԳƵġ�A2B2C2��
��3��������C����x��ĶԳƵ�P������P����ƽ��x��xȡ����������λ���Ⱥ����ڡ�A2B2C2���ڲ�����ֱ��д��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ε��ϵ�Ϊ![]() +2
+2![]() -10���µ�Ϊ3
-10���µ�Ϊ3![]() -5
-5![]() -80����Ϊ40.��
-80����Ϊ40.��![]() ȡ3��
ȡ3��
��1����ʽ�ӱ�ʾͼ����Ӱ���ֵ������
��2����![]() =10ʱ������Ӱ���������ֵ��
=10ʱ������Ӱ���������ֵ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com