
【题目】已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC

(1)如图1,若∠AOC=30°,求∠DOE的度数。
(2)如图1,若∠AOC=![]() ,直接写出∠DOE的度数。(用含的代数式表示)
,直接写出∠DOE的度数。(用含的代数式表示)
(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出结论,并说明理由。
(4)在图2中,若∠AOC内部有一条射线OF,且满足∠AOC-4∠AOF=2∠BOE,其它条件不变,试写出∠AOF与∠DOE度数的关系(不写过程)
【答案】(1)15°;(2)∠DOE=![]()
![]() ;(3)证明见解析;(4)∠DOE=∠AOF+45°.
;(3)证明见解析;(4)∠DOE=∠AOF+45°.
【解析】
(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)可得出结论∠DOE=![]() ∠AOC,从而用含a的代数式表示出∠DOE的度数;
∠AOC,从而用含a的代数式表示出∠DOE的度数;
(3)由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;
(4)设∠DOE=x,∠AOF=y,根据已知和:∠AOC-4∠AOF=2∠BOE,结合图形可得出∠DOE=∠AOF+45°.
解:(1)∵∠AOC=30∴∠COB=150,
又 ∵OE平分∠BOC, ∴∠COE=75,
而∠COD=90,∴∠DOE=15 ;
(2)∠DOE=![]()
![]() ;
;
(3)设∠AOC=![]() ,则∠BOC=180-
,则∠BOC=180-![]() ,
,
又∵OE平分∠BOC, ∴∠COE=![]() (180°-
(180°-![]() =90°-
=90°-![]()
![]() .
.
又∵∠DOE=90,
∴∠DOE=90-(90-![]()
![]() )=-
)=-![]()
![]() ,
,
∴∠DOE=-![]() ∠AOC ;
∠AOC ;
(4)∠DOE=∠AOF+45°.


科目:初中数学 来源: 题型:
【题目】如图是某班全体学生外出时选择乘车、步行、骑车人数的条形统计图和扇形统计图(两图都不完整),则下列结论中正确的是( )

A. 步行人数为30人 B. 骑车人数占总人数的10%
C. 该班总人数为50人 D. 乘车人数是骑车人数的40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=![]() .
.
(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=![]() .
.
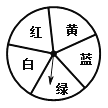
(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=![]() .
.
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOD中,∠AOD=90°,OA=6,点P为![]() 上任意一点(不与点A和D重合),
上任意一点(不与点A和D重合),
PQ⊥OD于点Q,点I为△OPQ的内心,过O、I和D三点的圆的半径为r,则当点P在![]() 上运动时,求r的值.
上运动时,求r的值.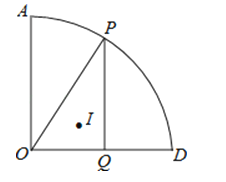
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲乙两人合作需要8天完成任务,若甲单独做需要12天完成任务.
(1)若甲乙两人一起做6天,剩下的由甲单独做,还需要几天完成?
(2)若甲乙两人一起做4天,剩下的由乙单独做,还需要几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,以AD为直径的半圆与BC相切于E,BO交半圆于F,DF的延长线交AB于点P,连DE.以下结论:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4ABDC.其中正确的是( )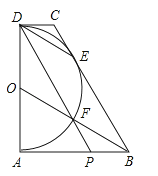
A.①②③④
B.只有①②
C.只有①②④
D.只有③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )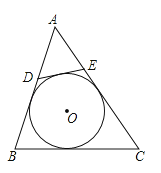
A.7
B.8
C.9
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一探究活动:如图1,有甲、乙两个三角形,甲三角形内角分别为10°,20°,150°;乙三角形内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形顶角的度数.
(1)小明按要求画出了图1中甲图的分割线,请你帮他作出图1中乙图的分割线;
(2)小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形;请在图2中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:正整数n的“H运算”是:①当n为奇数时,H=3n+13;②当n为偶数时,H=n![]() …(连续乘以
…(连续乘以![]() ,一直算到H为奇数止).如:数3经过“H运算”的结果是22,经过2次“H运算”的结果为11,经过三次“H运算”的结果为46,那么257经2017次“H运算”得到的结果是( )
,一直算到H为奇数止).如:数3经过“H运算”的结果是22,经过2次“H运算”的结果为11,经过三次“H运算”的结果为46,那么257经2017次“H运算”得到的结果是( )
A. 161 B. 1 C. 16 D. 以上答案均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com