
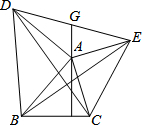
 在锐角三角形ABC中,AF是BC边上的高,分别以AB、AC为一边,向外作△ABD和△ACE,使得AB=AD,AC=AE,∠BAD=∠CAE=90°,连接BE、DE、DC,DE与FA的延长线交于点G,下列结论:①BE=DC;②BE⊥DC;③AG是△ADE的中线;④∠DAG=∠ABC.其中正确的有( )
在锐角三角形ABC中,AF是BC边上的高,分别以AB、AC为一边,向外作△ABD和△ACE,使得AB=AD,AC=AE,∠BAD=∠CAE=90°,连接BE、DE、DC,DE与FA的延长线交于点G,下列结论:①BE=DC;②BE⊥DC;③AG是△ADE的中线;④∠DAG=∠ABC.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①由已知条件可证明△ADC≌△ABE,可得到CD=BE;
②设BE和AC交于点R,可知∠AEB=∠ACD,结合对顶角和三角形内角和定理,可得到∠ENC=90°;
③过D作DH⊥AF交AF的延长线于H,过E作EM⊥AG于M,根据余角的性质得到∠H=∠AFB,求得∠HDA=∠BAF,证得△AHD≌△ABF,根据全等三角形的性质得到DH=AF,同理EM=AF,等量代换得到DH=EM,根据全等三角形的性质的得到DG=EG,即可得到结论;
④根据全等三角形的性质即可得到结论.
解答 解:①∵△ABD和△ACE为等腰直角三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC,
∴∠DAC=∠EAB,
在△ADC和△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠EAB}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△ABE(SAS),
∴CD=BE;故①正确;
设BE交AC于点R,CD,BE交于N如图1,
由①可知∠AEB=∠ACD,且∠ARE=∠NRC,
∴∠AER+∠ARE=∠NCR+∠NRC,
∴∠EFC=∠EAR=90°,
∴BE⊥DC;故②正确; ③过D作DH⊥AF交AF的延长线于H,过E作EM⊥AG于M,
③过D作DH⊥AF交AF的延长线于H,过E作EM⊥AG于M,
∵AF⊥BC,
∴∠AFB=90°,
∴∠H=∠AFB,
∵∠BAD=90°,
∴∠HDA=∠BAF,
在△AHD与△ABF中,$\left\{\begin{array}{l}{∠H=∠AFB}\\{∠HDA=∠BAF}\\{AD=AB}\end{array}\right.$,
∴△AHD≌△ABF,
∴DH=AF,
同理EM=AF,
∴DH=EM,
在△DHG与△EMG中,$\left\{\begin{array}{l}{∠H=∠EMG}\\{∠DGH=∠EGM}\\{DH=EM}\end{array}\right.$,
∴△DHG≌△EMG,
∴DG=EG,
∴AG是△ADE的中线;故③正确;
④∵△AHD≌△ABF,
∴∠DAG=∠ABC,故④正确.
故选A.
点评 本题主要考查全等三角形的判定和性质,等腰直角三角形的性质,三角形中线的定义,正确的作出辅助线是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
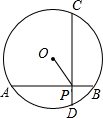 如图,⊙O的半径是6cm,弦AB=10cm,弦CD=8cm,且AB⊥CD于P,则OP的长是( )
如图,⊙O的半径是6cm,弦AB=10cm,弦CD=8cm,且AB⊥CD于P,则OP的长是( )| A. | $\sqrt{30}$cm | B. | $\sqrt{31}$cm | C. | 7cm | D. | 4$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
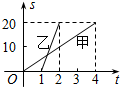 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前| A. | 乙比甲晚出发1小时 | B. | 甲比乙晚到B地3小时 | ||
| C. | 甲的速度是4千米/小时 | D. | 乙的速度是10千米/小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
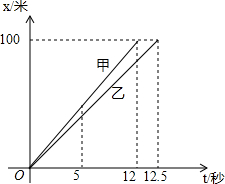 假定在一次赛跑中,甲、乙两人所行路程x与时间t的关系如图所示,那么可以知道:
假定在一次赛跑中,甲、乙两人所行路程x与时间t的关系如图所示,那么可以知道:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
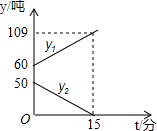 某空军加油飞机给另一架正在飞行的运输飞机进行空中加油,在加油的过程中,设运输飞机的油箱余油量为y1(吨).加油飞机的油箱余油量为y2(吨),已知y1(吨),y2(吨)与加油时间t(分)之间的函数关系图象如图所示.
某空军加油飞机给另一架正在飞行的运输飞机进行空中加油,在加油的过程中,设运输飞机的油箱余油量为y1(吨).加油飞机的油箱余油量为y2(吨),已知y1(吨),y2(吨)与加油时间t(分)之间的函数关系图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com