
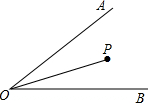
 如图所示,已知∠AOB为30°,点P在∠AOB内部,OP为10厘米,试在AOB两边上各找一点Q,R(均不与点O重合),求PR+PQ+QR的最小值.
如图所示,已知∠AOB为30°,点P在∠AOB内部,OP为10厘米,试在AOB两边上各找一点Q,R(均不与点O重合),求PR+PQ+QR的最小值.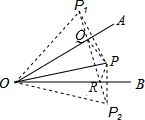 解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于Q,交OB于R,
解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于Q,交OB于R,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com