
分析 先算括号内的加法,同时把除法变成乘法,再算乘法,最后代入求出即可.
解答 解:($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$
=$\frac{{x}^{2}-y-x(x+1)}{x}$•$\frac{(x-y)^{2}}{(x+y)(x-y)}$
=-$\frac{x+y}{x}$•$\frac{x-y}{x+y}$
=-$\frac{x-y}{x}$
把$x=\sqrt{5},\;y=\sqrt{10}$代入得 原式=$\frac{\sqrt{5}-\sqrt{10}}{\sqrt{5}}$=$\sqrt{2}$-1.
点评 本题考查了分式的混合运算和求值,能正确根据分式的运用法则进行化简是解此题的关键,注意运算顺序.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
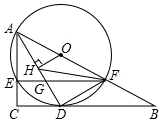 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
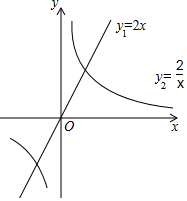 在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.
在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com