
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,过点
的弦,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() 于
于![]() ,且
,且![]() .
.
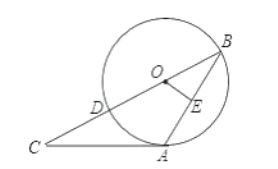
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)CD= 2.
【解析】
(1)连接OA,利用三角形中位线的性质,直角三角形中30°角所对的直角边与斜边的关系,即可证明
(2)由(1)可得AO=OD=2OE,再根据直角三角形中30°角所对的直角边与斜边的关系,可得出CD的值.
(1)证明:连接OA,
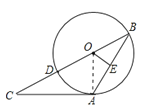
∵过点A的切线交BD延长线于点C,
∴OA⊥AC,
∴∠OAC=90°
∵OA=OB,
∴∠AOC=2∠B,
∵AB=AC,
∴∠B=∠C,
∵∠C+∠AOC=90°
∴∠B+2∠B=90°,
∴∠B =30°·
∵OE⊥AB,
∴∠OEB=90°,
∴OB=2OE,即2OE=r
(2)解:∵OE=1
∴AO=OD=2OE=2
∵∠C=∠B=30°,∠OAC=90°
∴OC=2AO=4
∴CD=OC-OD=2.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】某中学全体同学参加了“关怀贫困学生”爱心捐款活动,该校随机抽查了七、八、九三个年级部分学生捐款情况,将结果绘制成两幅不完整的统计图.根据图中的信息,解决下列问题:
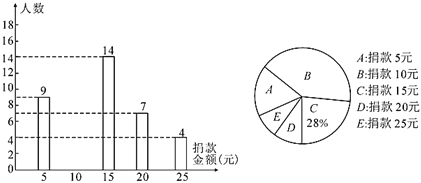
(1)这次共抽查了_______名学生进行统计,其中![]() 类所对应扇形的圆心角的度数为________;
类所对应扇形的圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校有![]() 名学生,估计该校捐款
名学生,估计该校捐款![]() 元的学生有多少人?
元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
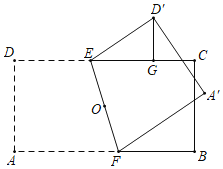
【题目】如图,点O是矩形ABCD的对角线的交点,AB=15,BC=8,直线EF经过点O,分别与边CD,AB相交于点E,F(其中0<DE<![]() ).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
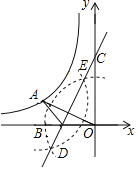
【题目】如图,点A在双曲线y=![]() (k<0)上,连接OA,分别以点O和点A为圆心,大于
(k<0)上,连接OA,分别以点O和点A为圆心,大于![]() OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
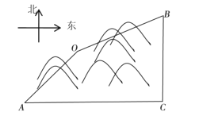
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起,高铁大大缩短了时空距离,改变了人们的出行方式,如图![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要绕行
地需要绕行![]() 地,若打通穿山隧道由
地,若打通穿山隧道由![]() 地到
地到![]() 地,再由
地,再由![]() 地到
地到![]() 地可大大缩短路程.
地可大大缩短路程.![]() ,
,![]() ,
,![]() ,
,![]() 公里,
公里,![]() 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
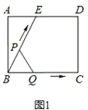
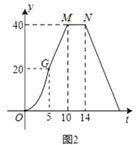
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止,设P、Q同时出发t秒时,BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示(其中曲线OG为抛物线的一部分,其余各部分均为线段)所示,则下列结论:①BEBC;②当t6秒时,ABE PQB;③点P运动了18秒;④当t![]() 秒时,ABE∽QBP.其中正确的是( ).
秒时,ABE∽QBP.其中正确的是( ).
A.①②B.①③④C.③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
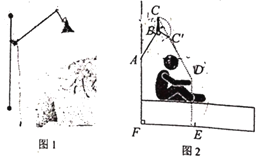
【题目】如图1是一款创意型壁灯,示意图如图2所示,∠BAF=150°,灯臂BC=0.2米,不使用时BC‖AF,人在床上阅读时,将![]() 绕点B旋转至
绕点B旋转至![]() ,
,![]() ,书本到地面距离DE=1米,C,
,书本到地面距离DE=1米,C,![]() ,D三点恰好在同一直线上,且
,D三点恰好在同一直线上,且![]() ,则此时固定点A到地面的距离
,则此时固定点A到地面的距离![]() ________米.
________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
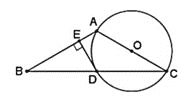
(1)求证:DE是⊙O的切线;
(2)若DE= ![]() ,∠C=30°,求
,∠C=30°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
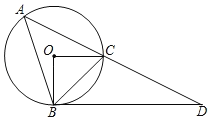
【题目】如果,⊙O是△ABC的外接圆,∠A=45°,BD∥OC交AC的延长线于点D.
(1)求证:BD是⊙O的切线;
(2)若∠D=30°,OC=2.
①求∠ABC的度数;
②求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com