
【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ![]() ,则a的值为 .
,则a的值为 .
【答案】-1
【解析】解:∵关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根, ∴ ![]() ,
,
解得:a<0,且a≠﹣2 ①
设抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,
则α、β是关于x的方程x2﹣(2a+1)x+2a﹣5=0的两个不相等的实数根,
∵△=[﹣(2a+1)]2﹣4×1×(2a﹣5)=(2a﹣1)2+21>0,
∴a为任意实数②
由根与系数关系得:α+β=2a+1,αβ=2a﹣5.
∵抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别位于点(2,0)的两旁,
∴α<2,β>2,
∴(α﹣2)(β﹣2)<0,
∴αβ﹣2(α+β)+4<0,
∴2a﹣5﹣2(2a+1)+4<0
解得:a>﹣ ![]() ③
③
由①、②、③得a的取值范围是﹣ ![]() <a<0;
<a<0;
∵x1和x2是关于x的方程(a+2)x2﹣2ax+a=0的两个不相等的实数根
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∵﹣ ![]() <a<0,
<a<0,
∴a+2>0,
∴x1x2= ![]() <0.
<0.
不妨设x1>0,x2<0,
∴|x1|+|x2|=x1﹣x2=2 ![]() ,
,
∴x12﹣2x1x2+x22=8,即(x1+x2)2﹣4x1x2=8,
∴( ![]() )2﹣
)2﹣ ![]() =8,
=8,
解这个方程,得:a1=﹣4,a2=﹣1,
经检验,a1=﹣4,a2=﹣1都是方程( ![]() )2﹣
)2﹣ ![]() =8的根.
=8的根.
∵a=﹣4<﹣ ![]() ,舍去,
,舍去,
∴a=﹣1为所求.
所以答案是﹣1.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A.B、C、D、E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A.E两点表示的数的分别为 -13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )
![]()
A. -2 B. -1 C. 0 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45° 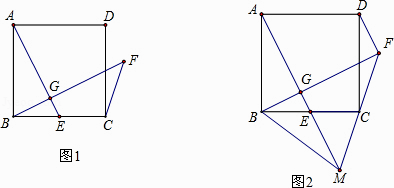
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长. 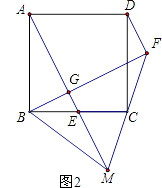
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是 . 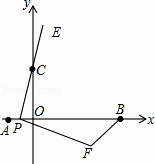
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP, 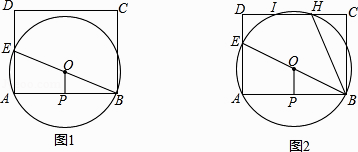
(1)求证:BE是⊙O的直径且OP⊥AB;
(2)若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;
(3)如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com