
”¾ĢāÄæ”æČēĶ¼1£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() Į½µć£¬Óė
Į½µć£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬
£¬![]() £¬¾ŲŠĪ
£¬¾ŲŠĪ![]() µÄ±ß
µÄ±ß![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() ½»Å×ĪļĻßÓŚµć
½»Å×ĪļĻßÓŚµć![]() .
.
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ČēĶ¼2£¬µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬¹żµć
ÉĻ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬¹żµć![]() ×÷
×÷![]() ÖįµÄĘ½ŠŠĻß½»Ö±Ļß
ÖįµÄĘ½ŠŠĻß½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() £¬×÷
£¬×÷![]() £¬“¹×ćĪŖ
£¬“¹×ćĪŖ![]() .Éč
.Éč![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() £¬µć
£¬µć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹĒ£Ø²»±ŲŠ“³ö
µÄŗÆŹż¹ŲĻµŹĒ£Ø²»±ŲŠ“³ö![]() µÄȔֵ·¶Ī§£©£¬²¢Ēó³ö
µÄȔֵ·¶Ī§£©£¬²¢Ēó³ö![]() µÄ×ī“óÖµ£»
µÄ×ī“óÖµ£»
£Ø3£©Čē¹ūµć![]() ŹĒÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄŅ»µć£¬Å×ĪļĻßÉĻŹĒ·ń“ęŌŚµć
ŹĒÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄŅ»µć£¬Å×ĪļĻßÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆŅŌ
£¬Ź¹µĆŅŌ![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ö±½ÓŠ“³öĖłÓŠĀś×ćĢõ¼žµÄ
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ö±½ÓŠ“³öĖłÓŠĀś×ćĢõ¼žµÄ![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.

”¾“š°ø”æ£Ø1£©Å×ĪļĻß½āĪöŹ½ĪŖy=©![]() x2©
x2©![]() x+2£»£Ø2£©l=©
x+2£»£Ø2£©l=©![]() £Øm+
£Øm+![]() £©2+
£©2+![]() £¬×ī“óÖµĪŖ
£¬×ī“óÖµĪŖ![]() £»£Ø3£©£Ø2£¬©
£»£Ø3£©£Ø2£¬©![]() £©»ņ£Ø©4£¬©
£©»ņ£Ø©4£¬©![]() £©»ņ£Ø©2£¬2£©£®
£©»ņ£Ø©2£¬2£©£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉĢõ¼žæÉĒóµĆA”¢BµÄ×ų±ź£¬ĄūÓĆ“ż¶ØĻµŹż·ØæÉĒóµĆÅ×ĪļĻß½āĪöŹ½£»
£Ø2£©æÉĻČĒóµĆEµć×ų±ź£¬“Ó¶ųæÉĒóµĆÖ±ĻßOE½āĪöŹ½£¬æÉÖŖ”ĻPGH=45”ć£¬ÓĆmæɱķŹ¾³öPGµÄ³¤£¬“Ó¶ųæɱķŹ¾³ölµÄ³¤£¬ŌŁĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹæÉĒóµĆĘä×ī“óÖµ£»
£Ø3£©·ÖACĪŖ±ßŗĶACĪŖ¶Ō½ĒĻߣ¬µ±ACĪŖ±ßŹ±£¬¹żM×÷¶Ō³ĘÖįµÄ“¹Ļߣ¬“¹×ćĪŖF£¬ŌņæÉÖ¤µĆ”÷MFN”Õ”÷AOC£¬æÉĒóµĆMµ½¶Ō³ĘÖįµÄ¾ąĄė£¬“Ó¶ųæÉĒóµĆMµćµÄŗį×ų±ź£¬æÉĒóµĆMµćµÄ×ų±ź£»µ±ACĪŖ¶Ō½ĒĻߏ±£¬ÉčACµÄÖŠµćĪŖK£¬æÉĒóµĆKµÄŗį×ų±ź£¬“Ó¶ųæÉĒóµĆMµÄŗį×ų±ź£¬“śČėÅ×ĪļĻß½āĪöŹ½æÉĒóµĆMµć×ų±ź£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ß¾ŲŠĪOBDCµÄ±ßCD=1£¬
”ąOB=1£¬
”ßAB=4£¬
”ąOA=3£¬
”ąA£Ø©3£¬0£©£¬B£Ø1£¬0£©£¬
°ŃA”¢BĮ½µć×ų±ź“śČėÅ×ĪļĻß½āĪöŹ½æɵĆ
![]() £¬
£¬
½āµĆ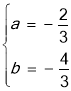 £¬
£¬
”ąÅ×ĪļĻß½āĪöŹ½ĪŖy=©![]() x2©
x2©![]() x+2£»
x+2£»
£Ø2£©ŌŚy=©![]() x2©
x2©![]() x+2ÖŠ£¬Įīy=2æɵĆ2=©
x+2ÖŠ£¬Įīy=2æɵĆ2=©![]() x2©
x2©![]() x+2£¬½āµĆx=0»ņx=©2£¬
x+2£¬½āµĆx=0»ņx=©2£¬
”ąE£Ø©2£¬2£©£¬
”ąÖ±ĻßOE½āĪöŹ½ĪŖy=©x£¬
ÓÉĢāŅāæɵĆP£Øm£¬©![]() m2©
m2©![]() m+2£©£¬
m+2£©£¬
”ßPG”ĪyÖį£¬
”ąG£Øm£¬©m£©£¬
”ßPŌŚÖ±ĻßOEµÄÉĻ·½£¬
”ąPG=©![]() m2©
m2©![]() m+2©£Ø©m£©=©
m+2©£Ø©m£©=©![]() m2©
m2©![]() m+2=©
m+2=©![]() £Øm+
£Øm+![]() £©2+
£©2+![]() £¬
£¬
”ßÖ±ĻßOE½āĪöŹ½ĪŖy=©x£¬
”ą”ĻPGH=”ĻCOE=45”ć£¬
”ąl=![]() PG=
PG=![]() [©
[©![]() £Øm+
£Øm+![]() £©2+
£©2+![]() ]=©
]=©![]() £Øm+
£Øm+![]() £©2+
£©2+![]() £¬
£¬
”ąµ±m=©![]() Ź±£¬lÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ
Ź±£¬lÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ![]() £»
£»
£Ø3£©¢Łµ±ACĪŖĘ½ŠŠĖıߊĪµÄ±ßŹ±£¬ŌņÓŠMN”ĪAC£¬ĒŅMN=AC£¬ČēĶ¼£¬¹żM×÷¶Ō³ĘÖįµÄ“¹Ļߣ¬“¹×ćĪŖF£¬ÉčAC½»¶Ō³ĘÖįÓŚµćL£¬
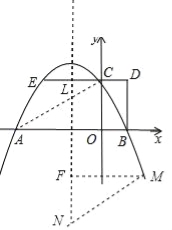
Ōņ”ĻALF=”ĻACO=”ĻFNM£¬
ŌŚ”÷MFNŗĶ”÷AOCÖŠ
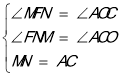
”ą”÷MFN”Õ”÷AOC£ØAAS£©£¬
”ąMF=AO=3£¬
”ąµćMµ½¶Ō³ĘÖįµÄ¾ąĄėĪŖ3£¬
ÓÖy=©![]() x2©
x2©![]() x+2£¬
x+2£¬
”ąÅ×ĪļĻ߶Ō³ĘÖįĪŖx=©1£¬
ÉčMµć×ų±źĪŖ£Øx£¬y£©£¬Ōņ|x+1|=3£¬½āµĆx=2»ņx=©4£¬
µ±x=2Ź±£¬y=©![]() £¬µ±x=©4Ź±£¬y=
£¬µ±x=©4Ź±£¬y=![]() £¬
£¬
”ąMµć×ų±źĪŖ£Ø2£¬©![]() £©»ņ£Ø©4£¬©
£©»ņ£Ø©4£¬©![]() £©£»
£©£»
¢Śµ±ACĪŖ¶Ō½ĒĻߏ±£¬ÉčACµÄÖŠµćĪŖK£¬
”ßA£Ø©3£¬0£©£¬C£Ø0£¬2£©£¬
”ąK£Ø©![]() £¬1£©£¬
£¬1£©£¬
”ßµćNŌŚ¶Ō³ĘÖįÉĻ£¬
”ąµćNµÄŗį×ų±źĪŖ©1£¬
ÉčMµćŗį×ų±źĪŖx£¬
”ąx+£Ø©1£©=2”Į£Ø©![]() £©=©3£¬½āµĆx=©2£¬“ĖŹ±y=2£¬
£©=©3£¬½āµĆx=©2£¬“ĖŹ±y=2£¬
”ąM£Ø©2£¬2£©£»
×ŪÉĻæÉÖŖµćMµÄ×ų±źĪŖ£Ø2£¬©![]() £©»ņ£Ø©4£¬©
£©»ņ£Ø©4£¬©![]() £©»ņ£Ø©2£¬2£©£®
£©»ņ£Ø©2£¬2£©£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø2015ÄĻĶØ£©ČēĶ¼£¬ŌŚABCDÖŠ£¬µćE£¬F·Ö±šŌŚAB£¬DCÉĻ£¬ĒŅED”ĶDB£¬FB”ĶBD£®
£Ø1£©ĒóÖ¤£ŗ”÷AED”Õ”÷CFB£»
£Ø2£©Čō”ĻA=30”ć£¬”ĻDEB=45”ć£¬ĒóÖ¤£ŗDA=DF£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ČēĶ¼£¬CDĪŖ”ŃOÖ±¾¶£¬CD”ĶABÓŚµćF£¬AE”ĶBCÓŚE£¬AE¹żŌ²ŠÄO£¬ĒŅAO=1£®ŌņĖıߊĪBEOFµÄĆ껿ĪŖ£Ø””””£©
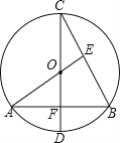
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø6·Ö£©ČēĶ¼£¬ĮāŠĪABCDµÄ¶Ō½ĒĻßAC£¬BDĻą½»ÓŚµćO£¬·Ö±šŃÓ³¤OA£¬OCµ½µćE£¬F£¬Ź¹AE=CF£¬ŅĄ“ĪĮ¬½ÓB£¬F£¬D£¬Eø÷µć£®

£Ø1£©ĒóÖ¤£ŗ”÷BAE”Õ”÷BCF£»
£Ø2£©Čō”ĻABC=50”ć£¬Ōņµ±”ĻEBA= ”揱£¬ĖıߊĪBFDEŹĒÕż·½ŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(12·Ö)(2017”¤»ĘøŌ)ŅŃÖŖ£ŗČēĶ¼£¬Ņ»“ĪŗÆŹży£½£2x£«1Óė·“±ČĄżŗÆŹży£½![]() µÄĶ¼ĻóÓŠĮ½øö½»µćA(£1£¬m)ŗĶB£¬¹żµćA×÷AE”ĶxÖį£¬“¹×ćĪŖE£»¹żµćB×÷BD”ĶyÖį£¬“¹×ćĪŖµćD£¬ĒŅµćDµÄ×ų±źĪŖ(0£¬£2)£¬Į¬½įDE.
µÄĶ¼ĻóÓŠĮ½øö½»µćA(£1£¬m)ŗĶB£¬¹żµćA×÷AE”ĶxÖį£¬“¹×ćĪŖE£»¹żµćB×÷BD”ĶyÖį£¬“¹×ćĪŖµćD£¬ĒŅµćDµÄ×ų±źĪŖ(0£¬£2)£¬Į¬½įDE.
(1)ĒókµÄÖµ£»
(2)ĒóĖıߊĪAEDBµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚx·½³Ģx2-6x+m+4=0ÓŠĮ½øöŹµŹżøłx1£¬x2
£Ø1£©ĒómµÄȔֵ·¶Ī§£®
£Ø2£©Čō![]() £¬ĒómµÄÖµ£®
£¬ĒómµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
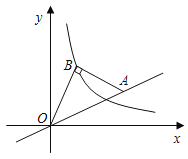
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy£½ax¾¹żµćA£Ø4£¬2£©£¬µćBŌŚĖ«ĒśĻßy£½![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£¬Į¬½įOB”¢AB£¬Čō”ĻABO£½90”ć£¬BA£½BO£¬ŌņkµÄÖµĪŖ_____£®
£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬Į¬½įOB”¢AB£¬Čō”ĻABO£½90”ć£¬BA£½BO£¬ŌņkµÄÖµĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½ax2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø4£¬0£©£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬2£©£¬¶Ō³ĘÖįx£½1£¬ÓėxÖį½»ÓŚµćH£®

£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©Ö±Ļßy£½kx+1£Øk”Ł0£©ÓėyÖį½»ÓŚµćE£¬ÓėÅ×ĪļĻß½»ÓŚµć P£¬Q£ØµćPŌŚyÖį×ó²ą£¬µćQŌŚyÖįÓŅ²ą£©£¬Į¬½ÓCP£¬CQ£¬Čō”÷CPQµÄĆ껿ĪŖ![]() £¬ĒóµćP£¬QµÄ×ų±ź£»
£¬ĒóµćP£¬QµÄ×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½ÓAC½»PQÓŚG£¬ŌŚ¶Ō³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µćK£¬Į¬½ÓGK£¬½«Ļ߶ĪGKČʵćGĖ³Ź±ÕėŠż×Ŗ90”ć£¬Ź¹µćKĒ”ŗĆĀäŌŚÅ×ĪļĻßÉĻ£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćKµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÅ×ĪļĻßy£½ax2+bx+c£Øa”Ł0£©ÓėxÖį½»ÓŚA£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬µćBŗĶµćCµÄ×ų±ź·Ö±šĪŖ£Ø3£¬0£©”¢£Ø0£¬©3£©£¬Å×ĪļĻߵĶŌ³ĘÖįĪŖx£½1£¬DĪŖÅ×ĪļĻߵĶ„µć£®
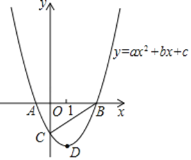
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©µćEĪŖĻ߶ĪBCÉĻŅ»¶Æµć£¬¹żµćE×÷xÖįµÄ“¹Ļߣ¬ÓėÅ×ĪļĻß½»ÓŚµćF£¬ĒóĖıߊĪACFBĆ껿µÄ×ī“óÖµ£¬ŅŌ¼°“ĖŹ±µćEµÄ×ų±ź£®
£Ø3£©Å×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µćP£¬Ź¹”÷PCDĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Š“³öµćPµćµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com