
【题目】某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图


(1)①在扇形图中,C部门所对应的圆心角的度数为
②在统计表中,b= ,c=
(2)求这个公司平均每人所创年利润.
【答案】(1)①108°;②b=9,c=6;(2)7.6万元
【解析】试题分析:(1)①根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可;②先求得A部门的员工人数所占的百分比,进而得到各部门的员工总人数,据此可得B,C部门的人数;
(2)根据总利润除以总人数,即可得到这个公司平均每人所创年利润.
试题解析:
(1)①在扇形图中,C部门所对应的圆心角的度数为:360°×30%=108°;
②A部门的员工人数所占的百分比为:1﹣30%﹣45%=25%,
各部门的员工总人数为:5÷25%=20(人),
∴b=20×45%=9,c=20×30%=6,
故答案为:108°,9,6;
(2)这个公司平均每人所创年利润为: ![]() (万元).
(万元).


科目:初中数学 来源: 题型:
【题目】阅读以下两则材料,解决后续问题:
材料一:我们可以将任意三位数记为![]() (其中a,b,c,分别表示该数的百位数字、十位数字和个位数字,且a≠0,显然
(其中a,b,c,分别表示该数的百位数字、十位数字和个位数字,且a≠0,显然![]() =100a+10b+c.
=100a+10b+c.
材料二:若一个三位数的三个数字均不为0且三个数字互不相等,则称之为原始数,比如123就是一个原始数.将原始数的三个数位数字交换顺序,可产生出5个新的原始数,比如由123可以产生出132、213、231、312、321这5个新原始数.将这6个数相加,得到的和1332称为由原始数123生成的终止数.
问题:(1)求原始数247生成的终止数;
(2)试说明所有的原始数生成的终止数都能被222整除;
(3)若一个原始数生成的终止数为![]() ,求满足条件的所有原始数.
,求满足条件的所有原始数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,

(1)求证:∠DHO=∠DCO.
(2)若OC=4,BD=6,求菱形ABCD的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
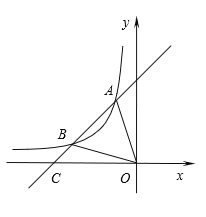
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人各射击![]() 次,甲所中的环数是
次,甲所中的环数是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且甲所中的环数的平均数是
,且甲所中的环数的平均数是![]() ,众数是
,众数是![]() ;乙所中的环数的平均数是
;乙所中的环数的平均数是![]() ,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )
,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )
A.甲射击成绩比乙稳定B.乙射击成绩比甲稳定
C.甲,乙射击成绩稳定性相同D.甲、乙射击成绩稳定性无法比较
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道![]() 表示5与(-2)之差的绝对值,也可理解为5与-2两数在数轴上所对的两点之间的距离,试探索:
表示5与(-2)之差的绝对值,也可理解为5与-2两数在数轴上所对的两点之间的距离,试探索:
(1) 求![]() = ;
= ;
(2) 使得![]() =3成立的数是 ;
=3成立的数是 ;
(3) 由以上探索猜想,对于任何有理数x,则![]() 最小值是 ;
最小值是 ;
(4)由以上探索猜想,使得![]() 的成立的整数x是
的成立的整数x是
查看答案和解析>>
科目:初中数学 来源: 题型:
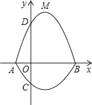
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节放假时,小华一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了4千米到超市买东西,然后又向东走了3千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
![]()
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)若小轿车每千米耗油0.09升,求小明一家从出发到返回家所经历路程小车的耗油量.(精确到0.1升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.


(1)当![]() 时,
时,![]() = ,
= ,![]() = ;点
= ;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐 (填“增大”或“减小”);
逐渐 (填“增大”或“减小”);
(2)当![]() 等于多少时,
等于多少时,![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出![]() 的度数.若不可以,请说明理由.
的度数.若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com