
 ĪŅĆĒÖŖµĄ£¬¾¹żŌµćµÄÅ×ĪļĻßæÉŅŌÓĆy=ax2+bx£Øa”Ł0£©±ķŹ¾£¬¶ŌÓŚÕāŃłµÄÅ×ĪļĻߣŗ
ĪŅĆĒÖŖµĄ£¬¾¹żŌµćµÄÅ×ĪļĻßæÉŅŌÓĆy=ax2+bx£Øa”Ł0£©±ķŹ¾£¬¶ŌÓŚÕāŃłµÄÅ×ĪļĻߣŗ·ÖĪö £Ø1£©°Ńµć£Ø-2£¬0£©ŗĶ£Ø-1£¬3£©·Ö±š“śČėy=ax2+bx£¬µĆµ½¹ŲÓŚa”¢bµÄ¶žŌŖŅ»“Ī·½³Ģ×飬½ā·½³Ģ×鼓æÉ£»
£Ø2£©øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬µĆ³öÅ×ĪļĻßy=ax2+bxµÄ¶„µć×ų±źŹĒ£Ø-$\frac{b}{2a}$£¬-$\frac{{b}^{2}}{4a}$£©£¬°Ń¶„µć×ų±ź“śČėy=-2x£¬µĆ³ö-$\frac{{b}^{2}}{4a}$=-2”Į£Ø-$\frac{b}{2a}$£©£¬¼“æÉĒó³öbµÄÖµ£»
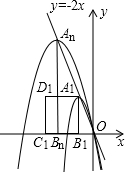
£Ø3£©ÓÉÓŚÕā×éÅ×ĪļĻߵĶ„µćA1”¢A2”¢”£¬AnŌŚÖ±Ļßy=-2xÉĻ£¬øł¾Ż£Ø2£©µÄ½įĀŪæÉÖŖ£¬b=4»ņb=0£®¢Łµ±b=0Ź±£¬²»ŗĻĢāŅāÉįČ„£»¢Śµ±b=-4Ź±£¬Å×ĪļĻߵıķ“ļŹ½ĪŖy=ax2-4x£®ÓÉĢāŅāæÉÖŖ£¬µŚnĢõÅ×ĪļĻߵĶ„µćĪŖAn£Ø-n£¬2n£©£¬ŌņDn£Ø-3n£¬2n£©£¬ŅņĪŖŅŌAnĪŖ¶„µćµÄÅ×ĪļĻß²»æÉÄܾ¹żµćDn£¬É赌n+k£ØkĪŖÕżÕūŹż£©ĢõÅ×ĪļĻß¾¹żµćDn£¬“ĖŹ±µŚn+kĢõÅ×ĪļĻߵĶ„µć×ų±źŹĒAn+k£Ø-n-k£¬2n+2k£©£¬øł¾Ż-$\frac{b}{2a}$=-n-k£¬µĆ³öa=$\frac{b}{2£Øn+k£©}$=-$\frac{2}{n+k}$£¬¼“µŚn+kĢõÅ×ĪļĻߵıķ“ļŹ½ĪŖy=-$\frac{2}{n+k}$x2-4x£¬øł¾ŻDn£Ø-3n£¬2n£©ŌŚµŚn+kĢõÅ×ĪļĻßÉĻ£¬µĆµ½2n=-$\frac{2}{n+k}$”Į£Ø-3n£©2-4”Į£Ø-3n£©£¬½āµĆk=$\frac{4}{5}$n£¬½ų¶ųĒó½ā¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©”ßÅ×ĪļĻßy=ax2+bx¾¹żµć£Ø-2£¬0£©ŗĶ£Ø-1£¬3£©£¬
”ą$\left\{\begin{array}{l}{4a-2b=0}\\{a-b=3}\end{array}\right.$£¬½āµĆ$\left\{\begin{array}{l}{a=-3}\\{b=-6}\end{array}\right.$£¬
”ąÅ×ĪļĻߵıķ“ļŹ½ĪŖy=-3x2-6x£»
£Ø2£©”ßÅ×ĪļĻßy=ax2+bxµÄ¶„µć×ų±źŹĒ£Ø-$\frac{b}{2a}$£¬-$\frac{{b}^{2}}{4a}$£©£¬ĒŅøƵćŌŚÖ±Ļßy=-2xÉĻ£¬
”ą-$\frac{{b}^{2}}{4a}$=-2”Į£Ø-$\frac{b}{2a}$£©£¬
”ßa”Ł0£¬”ą-b2=4b£¬
½āµĆb1=-4£¬b2=0£»
£Ø3£©Õā×éÅ×ĪļĻߵĶ„µćA1”¢A2”¢”£¬AnŌŚÖ±Ļßy=-2xÉĻ£¬
ÓÉ£Ø2£©æÉÖŖ£¬b=4»ņb=0£®
¢Łµ±b=0Ź±£¬Å×ĪļĻߵĶ„µćŌŚ×ų±źŌµć£¬²»ŗĻĢāŅā£¬ÉįČ„£»
¢Śµ±b=-4Ź±£¬Å×ĪļĻߵıķ“ļŹ½ĪŖy=ax2-4x£®
ÓÉĢāŅāæÉÖŖ£¬µŚnĢõÅ×ĪļĻߵĶ„µćĪŖAn£Ø-n£¬2n£©£¬ŌņDn£Ø-3n£¬2n£©£¬
”ßŅŌAnĪŖ¶„µćµÄÅ×ĪļĻß²»æÉÄܾ¹żµćDn£¬É赌n+k£ØkĪŖÕżÕūŹż£©ĢõÅ×ĪļĻß¾¹żµćDn£¬“ĖŹ±µŚn+kĢõÅ×ĪļĻߵĶ„µć×ų±źŹĒAn+k£Ø-n-k£¬2n+2k£©£¬
”ą-$\frac{b}{2a}$=-n-k£¬”ąa=$\frac{b}{2£Øn+k£©}$=-$\frac{2}{n+k}$£¬
”ąµŚn+kĢõÅ×ĪļĻߵıķ“ļŹ½ĪŖy=-$\frac{2}{n+k}$x2-4x£¬
”ßDn£Ø-3n£¬2n£©ŌŚµŚn+kĢõÅ×ĪļĻßÉĻ£¬
”ą2n=-$\frac{2}{n+k}$”Į£Ø-3n£©2-4”Į£Ø-3n£©£¬½āµĆk=$\frac{4}{5}$n£¬
”ßn£¬kĪŖÕżÕūŹż£¬ĒŅn”Ü12£¬
”ąn1=5£¬n2=10£®
µ±n=5Ź±£¬k=4£¬n+k=9£»
µ±n=10Ź±£¬k=8£¬n+k=18£¾12£ØÉįČ„£©£¬
”ąD5£Ø-15£¬10£©£¬
”ąÕż·½ŠĪµÄ±ß³¤ŹĒ10£®
µćĘĄ ±¾ĢāŹĒ¶ž“ĪŗÆŹż×ŪŗĻĢā£¬ĘäÖŠÉę¼°µ½ĄūÓĆ“ż¶ØĻµŹż·ØĒóÅ×ĪļĻߵĽāĪöŹ½£¬¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬ŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷£¬Õż·½ŠĪµÄŠŌÖŹµČÖŖŹ¶£¬ÓŠŅ»¶ØÄŃ¶Č£®É赌n+k£ØkĪŖÕżÕūŹż£©ĢõÅ×ĪļĻß¾¹żµćDn£¬ÓĆŗ¬nµÄ“śŹżŹ½±ķŹ¾DnµÄ×ų±źŅŌ¼°ÓĆŗ¬n”¢kµÄ“śŹżŹ½±ķŹ¾µŚn+kĢõÅ×ĪļĻߏĒ½āĢāµÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ĪŖČĪŅāÕūŹż | B£® | ĪŖČĪŅāøŗÕūŹż | ||
| C£® | µČÓŚ0»ņĪŖČĪŅā²»µČÓŚ-1µÄøŗÕūŹż | D£® | ĪŖ²»µČÓŚ-1µÄ·ĒÕżÕūŹż |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | Č«ĻŲµÄČ«Ģå°ĖÄź¼¶Ń§Éś | |
| B£® | Č«ĻŲµÄČ«Ģå°ĖÄź¼¶Ń§ÉśĘŚÄ©ŹżŃ§æ¼ŹŌ³É¼Ø | |
| C£® | ³éČ”µÄ200Ćūѧɜ | |
| D£® | ³éČ”µÄ200ĆūѧɜʌĩŹżŃ§æ¼ŹŌ³É¼Ø |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
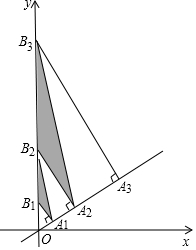 ČēĶ¼£¬Ö±Ļßy=$\frac{{\sqrt{3}}}{3}$xÉĻÓŠµćA1£¬A2£¬A3£¬”An+1£¬ĒŅOA1=1£¬A1A2=2£¬A2A3=4£¬AnAn+1=2n£¬·Ö±š¹żµćA1£¬A2£¬A3£¬”An+1×÷Ö±Ļßy=$\frac{{\sqrt{3}}}{3}$xµÄ“¹Ļߣ¬½»yÖįÓŚµćB1£¬B2£¬B3£¬”Bn+1£¬ŅĄ“ĪĮ¬½ÓA1B2£¬A2B3£¬A3B4£¬”AnBn+1£¬µĆµ½”÷A1B1B2£¬”÷A2B2B3£¬”÷A3B3B4£¬”£¬”÷AnBnBn+1£¬Ōņ”÷AnBnBn+1µÄĆ껿ĪŖ£Ø22n-1-2n-1£©$\sqrt{3}$£®£ØÓĆŗ¬ÕżÕūŹżnµÄŹ½×Ó±ķŹ¾£©
ČēĶ¼£¬Ö±Ļßy=$\frac{{\sqrt{3}}}{3}$xÉĻÓŠµćA1£¬A2£¬A3£¬”An+1£¬ĒŅOA1=1£¬A1A2=2£¬A2A3=4£¬AnAn+1=2n£¬·Ö±š¹żµćA1£¬A2£¬A3£¬”An+1×÷Ö±Ļßy=$\frac{{\sqrt{3}}}{3}$xµÄ“¹Ļߣ¬½»yÖįÓŚµćB1£¬B2£¬B3£¬”Bn+1£¬ŅĄ“ĪĮ¬½ÓA1B2£¬A2B3£¬A3B4£¬”AnBn+1£¬µĆµ½”÷A1B1B2£¬”÷A2B2B3£¬”÷A3B3B4£¬”£¬”÷AnBnBn+1£¬Ōņ”÷AnBnBn+1µÄĆ껿ĪŖ£Ø22n-1-2n-1£©$\sqrt{3}$£®£ØÓĆŗ¬ÕżÕūŹżnµÄŹ½×Ó±ķŹ¾£©²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ÕżĮł±ßŠĪABCDEFÄŚ½ÓÓŚ”ŃO£¬”ŃOµÄ°ė¾¶ĪŖ6£¬ŌņÕāøöÕżĮł±ßŠĪµÄ±ßŠÄ¾ąOMµÄ³¤ĪŖ3$\sqrt{3}$£®
ČēĶ¼£¬ÕżĮł±ßŠĪABCDEFÄŚ½ÓÓŚ”ŃO£¬”ŃOµÄ°ė¾¶ĪŖ6£¬ŌņÕāøöÕżĮł±ßŠĪµÄ±ßŠÄ¾ąOMµÄ³¤ĪŖ3$\sqrt{3}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1»ņ-4 | B£® | -1»ņ-4 | C£® | -1»ņ4 | D£® | 1»ņ4 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
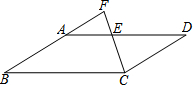 ČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬µćEŌŚAD±ßÉĻ£¬Į¬½ÓCE²¢ŃÓ³¤£¬½»BAµÄŃÓ³¤ĻßÓŚµćF£®ČōAE=$\frac{5}{8}$ED£¬Ōņ$\frac{FA}{AB}$µÄÖµĪŖ£Ø””””£©
ČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬µćEŌŚAD±ßÉĻ£¬Į¬½ÓCE²¢ŃÓ³¤£¬½»BAµÄŃÓ³¤ĻßÓŚµćF£®ČōAE=$\frac{5}{8}$ED£¬Ōņ$\frac{FA}{AB}$µÄÖµĪŖ£Ø””””£©| A£® | $\frac{15}{13}$ | B£® | $\frac{8}{5}$ | C£® | $\frac{5}{8}$ | D£® | $\frac{15}{8}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com