已知关于x的方程x2-2mx+n2=0
(1)若m从0,1,2,3四个数任意取一个数,n从0,1,2三个数任意取一个数,则方程有实数根的概率是多少?
(2)当m=2,n=1时,解此方程.
解:(1)∵关于x的方程x
2-2mx+n
2=0有实数根,
∴△>0,即4m
2-4n
2≥0,
∴m
2≥n
2,
画树状图:
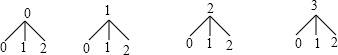
m从0,1,2,3四个数任意取一个数,n从0,1,2三个数任意取一个数,共有12种等可能的结果,
其中满足m
2≥n
2占9种,
所以方程有实数根的概率=
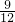
=

;
(2)当m=2,n=1时,方程为:x
2-4x+1=0,
x
2-4x+4=3,
∴(x-2)
2=3,
∴x-2=±

,
∴x
1=2+

,x
2=2-

.
分析:(1)根据一元二次方程ax
2+bx+c=0(a≠0)的根的判别式△的意义得到当△>0时,即4m
2-4n
2≥0,关于x的方程x
2-2mx+n
2=0有实数根,则m
2≥n
2;然后画树状图展示m从0,1,2,3四个数任意取一个数,n从0,1,2三个数任意取一个数的所有等可能的结果数为12,其中满足m
2≥n
2占9种,再根据概率的定义计算即可;
(2)把m=2,n=1代入方程得到x
2-4x+1=0,配方得到(x-2)
2=3,然后利用直接开平方法解方程即可.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0)的根的判别式△=b
2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了不等式的解法.

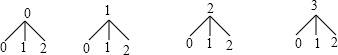
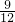 =
= ;
; ,
, ,x2=2-
,x2=2- .
.
