
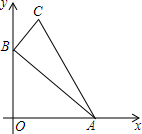
 如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.
如图,A(3,0),B(0,3),C(1,4),求△ABC的面积. 分析 过点C作DE垂直于y轴,作AE垂直于x轴,AE与DE相较于点E,这样就将△ABC就处于矩形OAED的内部,只要算出矩形OAED的面积,再求出△DBC,△CAE,△BOD的面积,就可以求得△ABC的面积.
解答 解:如下图,过点C作DE垂直于y轴,作AE垂直于x轴,AE与DE相较于点E.
∵A(3,0),B(0,3),C(1,4).
∴点D为(0,4),E为(3,4).
∴BD=1,CE=2,CD=1,AE=4,OA=3,OB=3.
∴S矩形OAED=OA•AE=3×4=12,
${S}_{△BOA}=\frac{1}{2}OA•OB=\frac{1}{2}×3×3=\frac{9}{2}$,
${S}_{△DBC}=\frac{1}{2}DB•DC=\frac{1}{2}×1×1=\frac{1}{2}$,
${S}_{△ACE}=\frac{1}{2}AE•CE=\frac{1}{2}×4×2=4$,
∴S△ABC=S矩形OAED-S△BOA-S△DBC$-{S}_{△ACE}=12-\frac{9}{2}-\frac{1}{2}-4=3$.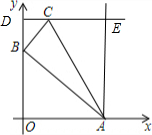
点评 本题考查三角形的面积,关键是在平面直角坐标系中,如何将三角形面积通过转化的数学思想,放在一个大的矩形之中,根据各点坐标,求出组成矩形的各个三角形的面积,从而求得我们所要求的三角形的面积.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
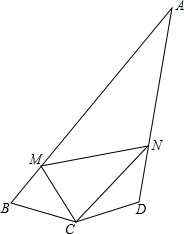 如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.
如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
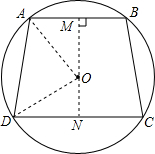 如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.
如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com