
【题目】如图①,我们在“格点”直角坐标系上可以看到,要求AB或CD的长度,可以转化为求Rt△ABC或Rt△DEF的斜边长.
例如:从坐标系中发现:D(﹣7,3),E(4,﹣3),所以DF=|5﹣(﹣3)|=8,EF=|4﹣(﹣7)|=11,所以由勾股定理可得:DE=![]() .
.
(1)在图①中请用上面的方法求线段AB的长:AB= ;
(2)在图②中:设A(x1,y1),B(x2,y2),试用x1,x2,y1,y2表示:AC= ,BC= ,AB= ;
(3)试用(2)中得出的结论解决如下题目:已知:A(2,1),B(4,3);
①直线AB与x轴交于点D,求线段BD的长;
②C为坐标轴上的点,且使得△ABC是以AB为边的等腰三角形,请求出C点的坐标.

【答案】(1)5;(2)AC=y1﹣y2;BC=x1﹣x2,AB=![]() ;(3)①
;(3)①![]() ;②(0,
;②(0,![]() ).
).
【解析】
(1)根据图①确定出BC与AC的长,利用勾股定理求出AB的长即可;
(2)在图②中,由A与B的坐标表示出AC,BC,利用勾股定理表示出AB的长即可;
(3)①利用题中的方法,根据D与B坐标求出DB的长即可;
②设C(0,y),由题意得到AC=BC,根据A与B坐标,利用题中的方法列出方程,求出方程的解得到y的值,即可确定出C坐标.
(1)根据题意得:AB=![]() =5;
=5;
(2)根据题意得:AC=y1-y2;BC=x1-x2,AB=![]() ;
;
(3)①∵A(2,1),B(4,3),
设直线AB的解析式为:y=kx+b,
可得:![]() ,
,
解得:![]() ,
,
所以直线AB的解析式为:y=x-1
把y=0代入y=x-1,
可得:x=1,
所以点D的坐标为(1,0),
所以BD=![]() =3
=3![]() ;
;
②设C坐标为(0,y),A(2,1),B(4,3),
根据题意得:AC=BC,即![]() ,
,
解得:y=5,
则C坐标为(0,5).


科目:初中数学 来源: 题型:
【题目】 如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省元. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:要设计一副宽20厘米、长30厘米的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形图案面积的![]() ,那么横彩条的宽度为多少厘米,竖彩条的宽度为多少厘米?
,那么横彩条的宽度为多少厘米,竖彩条的宽度为多少厘米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
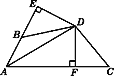
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8. 
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E,求由线段ED,BE, ![]() 所围成区域的面积.(其中
所围成区域的面积.(其中 ![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com