
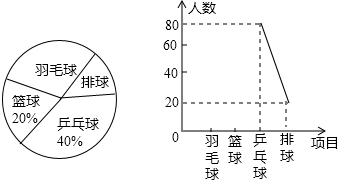
分析 (1)读图可知喜欢乒乓球的有80人,占40%.所以一共调查了80÷40%=200人;
(2)根据总人数和篮球所占百分比求得篮球的人数,由总人数求得与羽毛球人数,从而得出其所占的圆心角为360°×30%=108°;
(3)利用样本估计总体的办法,计算出答案即可.
解答 解:(1)本题调查的学生人数为80÷40%=200人,
故答案为:200;
(2)∵篮球的人数为200×20%=40人,
∴羽毛球的人数为200-40-80-20=60人,
则“羽毛球”所在的扇形的圆心角是$\frac{60}{200}$×360°=108°,
故答案为:108;
(3)补全图形如下: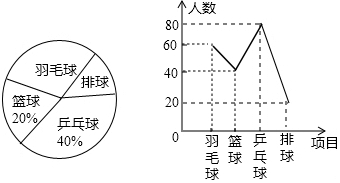
(4)1200×40%=480,
答:估计爱好乒乓球运动的约有480名学生.
点评 本题考查学生的读图能力以及频率、频数的计算.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
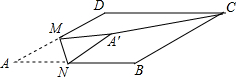 如图,在平行四边形ABCD中,∠BCD=30°,BC=6,CD=$6\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线
如图,在平行四边形ABCD中,∠BCD=30°,BC=6,CD=$6\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线查看答案和解析>>
科目:初中数学 来源: 题型:选择题
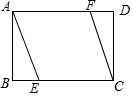 如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )
如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )| A. | $\sqrt{5}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{13}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
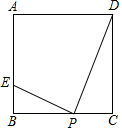 如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )| A. | 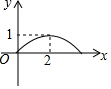 | B. | 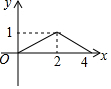 | C. | 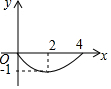 | D. | 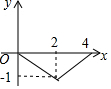 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2xy}{{x}^{2}-{y}^{2}}$ | B. | $-\frac{2xy}{{x}^{2}-{y}^{2}}$ | C. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
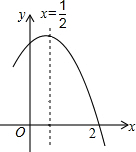 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0).下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-$\frac{5}{2}$,y1),($\frac{5}{2}$,y2)是抛物线上的两点,则y1<y2;⑤$\frac{1}{4}$a+$\frac{1}{2}$b>m(am+b)(其中m≠$\frac{1}{2}$).其中说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0).下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-$\frac{5}{2}$,y1),($\frac{5}{2}$,y2)是抛物线上的两点,则y1<y2;⑤$\frac{1}{4}$a+$\frac{1}{2}$b>m(am+b)(其中m≠$\frac{1}{2}$).其中说法正确的是( )| A. | ①②④⑤ | B. | ③④ | C. | ①③ | D. | ①②⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com