
分析 (1)解:设每台甲种空气净化器为x元,乙种净化器为(x+300)元,根据用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同,列出方程求解即可;
(2)设甲种空气净化器为y台,乙种净化器为(30-y)台,根据进货花费不超过42000元,列出不等式求解即可.
解答 (1)解:设每台甲种空气净化器为x元,乙种净化器为(x+300)元,由题意得:
$\frac{6000}{x}$=$\frac{7500}{x+300}$,
解得:x=1200,
经检验得:x=1200是原方程的解,
则x+300=1500,
答:每台甲种空气净化器、每台乙种空气净化器的进价分别为1200元,1500元.
(2)设甲种空气净化器为y台,乙种净化器为(30-y)台,根据题意得:
1200y+1500(30-y)≤42000,
y≥10,
答:至少进货甲种空气净化器10台.
点评 本题考查分式方程和不等式的应用,分析题意,找到合适的等量关系列出方程和不等式是解决问题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
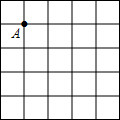 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+3的图象经过点(3,0).
已知二次函数y=x2+bx+3的图象经过点(3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com