已知△ABC.分别以AB和AC为斜边作等腰直角三角形.若AB=AC.向△ABC的外侧作等腰直角三角形.如图1所示.其中DF⊥AB于点F.EG⊥AC于点G.M是BC的中点.连接MD和ME．(1)下列结论正确的是①②③④①∠DAB=∠DMB,②整个图形是轴对称图形,③MD=ME,④AF=AG=$\frac{1}{2}$AB．(2)若AB=AC.仍分别以AB和AC为斜边.向△ABC的� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

7．已知△ABC，分别以AB和AC为斜边作等腰直角三角形，若AB=AC，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME．
（1）下列结论正确的是①②③④（填序号即可）
①∠DAB=∠DMB；②整个图形是轴对称图形；③MD=ME；④AF=AG=$\frac{1}{2}$AB．
（2）若AB=AC，仍分别以AB和AC为斜边，向△ABC的内侧作等腰支架你三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状为等腰直角三角形．

分析（1）由条件可以通过三角形全等和轴对称的性质，直角三角形的性质就可以得出结论；
（2）如图3，取AB、AC的中点F、G，连接DF，MF，EG，MG，DF和MG相交于H，根据三角形的中位线的性质K可以得出△DFM≌△MGE，由全等三角形的性质就可以得出结论；

解答解：（1）连接AM、FM、
∵AB=AC，BM=MC，
∴AM⊥BC，
∴∠AMB=∠ADB=90°，
∵AF=BF，
∴DF=AF=BF=FM，
∴A、D、B、M四点共圆，
∴∠BAD=∠BMD，故①正确，
∵△ADB和△AEC是等腰直角三角形，
∴∠ABD=∠DAB=∠ACE=∠EAC=45°，∠ADB=∠AEC=90°
在△ADB和△AEC中，
$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{∠ABD=∠ACE}\\{AB=AC}\end{array}\right.$，
∴△ADB≌△AEC（AAS），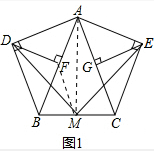
∴BD=CE，AD=AE，
∵DF⊥AB于点F，EG⊥AC于点G，
∴AF=BF=DF=$\frac{1}{2}$AB，AG=GC=GE=$\frac{1}{2}$AC．
∵AB=AC，
∴AF=AG=$\frac{1}{2}$AB，故④正确；
∵M是BC的中点，
∴BM=CM．
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABC+∠ABD=∠ACB+∠ACE，
即∠DBM=∠ECM．
在△DBM和△ECM中，
$\left\{\begin{array}{l}{BD=CE}\\{∠DBM=∠ECM}\\{BM=CM}\end{array}\right.$，
∴△DBM≌△ECM（SAS），
∴MD=ME．故③正确；
连接AM，根据前面的证明可以得出将图形1，沿AM对折左右两部分能完全重合，
∴整个图形是轴对称图形，故②正确．
故答案为：①②③④．

如图3，取AB、AC的中点F、G，连接DF，MF，EG，MG，
∵点M、F、G分别是BC、AB、AC的中点，
∴MF∥AC，MF=$\frac{1}{2}$AC，MG∥AB，MG=$\frac{1}{2}$AB，
∴四边形MFAG是平行四边形，
∴MG=AF，MF=AG．∠AFM=∠AGM．
∵△ADB和△AEC是等腰直角三角形，
∴DF=AF，GE=AG，∠AFD=∠BFD=∠AGE=90°
∴MF=EG，DF=MG，∠AFM-∠AFD=∠AGM-∠AGE，
即∠DFM=∠MGE．
在△DFM和△MGE中
$\left\{\begin{array}{l}{MF=EG}\\{∠DFM=∠MGE}\\{DF=MG}\end{array}\right.$，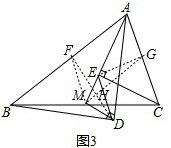
∴△DFM≌△MGE（SAS），
∴MD=ME，∠MDF=∠EMG．
∵MG∥AB，
∴∠MHD=∠BFD=90°，
∴∠HMD+∠MDF=90°，
∴∠HMD+∠EMG=90°，
即∠DME=90°，
∴△DME为等腰直角三角形；
故答案为等腰直角三角形．

点评本题考查了等腰直角三角形的性质的运用，等腰三角形的性质的运用，全等三角形的判定及性质的运用，三角形的中位线的性质的运用，直角三角形的斜边上的中线的性质的运用，平行四边形的判定及性质的运用，解答时根据三角形的中位线的性质制造全等三角形是解答本题的关键．

练习册系列答案

寒假百分百云南科技出版社系列答案

黄金假期寒假作业武汉大学出版社系列答案

寒假期导航学年知识大归纳辽海出版社系列答案

寒假生活湖南少年儿童出版社系列答案

寒假生活安徽教育出版社系列答案

寒假作业西南师范大学出版社系列答案

桂壮红皮书寒假作业河北人民出版社系列答案

寒假课程练习南方出版社系列答案

一路领先寒假作业河北美术出版社系列答案

开心寒假西南师范大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

17．

如图，数轴的单位长度为1，如果R，T表示的数互为相反数，那么图中的4个点中，点表示的数的绝对值最大的点是（填写点对应的字母即可）P．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．观察下列式子：
1=2×$\frac{0}{1}$+1
2=3×$\frac{1}{2}$+$\frac{1}{2}$
3=4×$\frac{2}{3}$+$\frac{1}{3}$
4=5×$\frac{3}{4}$+$\frac{1}{4}$
（1）根据上述规律，请猜想，若n为正整数，则n=（n+1）$\frac{n-1}{n}$+$\frac{1}{n}$；
（2）证明你猜想的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．若a＜0，b＞0，化简|b-a+1|+|a-b-5|的结果为（　　）

A．

B．

-2a+2b+6

C．

-4

D．

不能确定

查看答案和解析>>

科目：初中数学 来源： 题型：解答题