
【题目】(已知:如图,AB为⊙O的直径,AC、BC为弦,点P为![]() 上一点,AB=10,AC:BC=3:4.
上一点,AB=10,AC:BC=3:4.
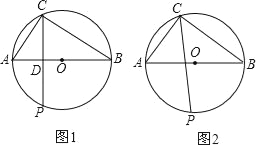
(1)当点P与点C关于直线AB对称时(如图1),求PC的长;
(2)当点P为![]() 的中点时(如图2),求PC的长.
的中点时(如图2),求PC的长.
【答案】(1)PC=9.6;(2)PC=![]() .
.
【解析】
(1)根据题意求得PC⊥AB,且CD=DP.然后根据勾股定理求出CD的长;
(2)过点B作BE⊥PC于点E,连接PB,由(1)问求出AC和BC的长,然后根据题干条件求出EP的长,即可求出PC.
(1)在⊙O中,如图
∵AB是直径,
∴![]()
∵点P与点C关于AB对称,
∴PC⊥AB,且CD=DP.
∴由三角形面积得:CDAB=ACBC.
∵AB=10,AC:BC=3:4,
∴由勾股定理求得AC=6,BC=8.
∴![]()
∴PC=2CD=9.6;
(2)过点B作BE⊥PC于点E,连接PB,
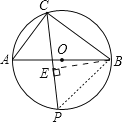
由(1)得AC=6,BC=8.
∵点P为弧AB的中点,∴![]()
在Rt△BEC中,可求得![]()
∵∠A=∠P,![]()
∴tan∠P=tan∠A.
∴![]()
∴![]()
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片![]() 和
和![]() .将这两张三角形胶片的顶点B与顶点E重合,把
.将这两张三角形胶片的顶点B与顶点E重合,把![]() 绕点B顺时针方向旋转,这时AC与DF相交于点O.
绕点B顺时针方向旋转,这时AC与DF相交于点O.
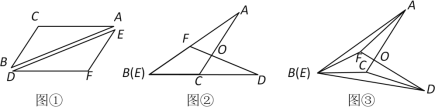
(1)当![]() 旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
(2)当![]() 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO,AD,探索BO与AD之间有怎样的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN.
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别为A(﹣1,﹣1),B(﹣4,﹣2),C(﹣1,﹣4).
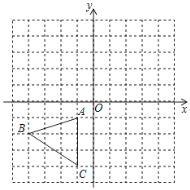
(1)点A关于y轴对称的点的坐标是;
(2)画出△ABC关于x轴对称的△A1B1C1分别写出点A1,B1,C1的坐标;
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发沿相同的路线匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:①A、B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的是________(填序号).
.其中正确的是________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师从学校出发,到距学校![]() 的某商场去给学生买奖品,他先步行了
的某商场去给学生买奖品,他先步行了![]() 后,换骑上了共享单车,到达商场时,全程总共刚好花了
后,换骑上了共享单车,到达商场时,全程总共刚好花了![]() .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).
.已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).
(1)求王老师步行和骑共享单车的平均速度分别为多少?
(2)买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出了2个小正方形(如图①),其中,3个正方形围成的三角形是直角三角形.再经过一次“生长”后,又生出了4个小正方形(如图②),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”,在“生长”了2019次后形成的图形中所有正方形的面积和是( )

A.2018B.2019C.2020D.2021
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在y轴正半轴上,点B与点C都在x轴上,且点B在点C的左侧,满足BC=OA,若-3am-1b2与anb2n-2是同类项且OA=m,OB=n.
(1)m= ;n= .
(2)点C的坐标是 .
(3)若坐标平面内存在一点D,满足△BCD全等△ABO,试求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com