
����Ŀ��ij������ɲ������ʻ�ľ���s����λ���ף���ʱ��t����λ���룩֮��Ĺ�ϵ�ò����������±���
ʱ��t���룩 | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | �� |
��ʻ����s���ף� | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | �� |
�������ֱ仯����һֱ����������ֹͣ��
��1��������Щ�����ڸ���������ϵ�л�����Ӧ�ĵ㣻
��2��ѡ���ʵ��ĺ�����ʾs��t֮��Ĺ�ϵ�������Ӧ�ĺ�������ʽ��
��3����ɲ����������ʻ�˶�����ֹͣ�� �ڵ�t�ֱ�Ϊt1 �� t2��t1��t2��ʱ����Ӧs��ֵ�ֱ�Ϊs1 �� s2 �� ��Ƚ� ![]() ��
�� ![]() �Ĵ�С�������ͱȽϽ����ʵ�����壮
�Ĵ�С�������ͱȽϽ����ʵ�����壮
���𰸡�
��1���⣺���ͼ��ʾ������ͼ����ȷ�����֣���
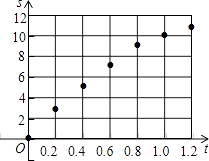
��2���⣺��ɢ��ͼ��֪�ú���Ϊ���κ���
����κ����Ľ���ʽΪ��s=at2+bt+c��
�������߾����㣨0��0����
��c=0��
���ɵ㣨0.2��2.8������1��10���ɵã� ![]()
��ã�a=��5��b=15��
����κ����Ľ���ʽΪ��s=��5t2+15t��
�����飬����������s=��5t2+15t��
��3���⣺������ɲ����ֹͣʱ�ľ��뼴�������е������룬
��t=�� ![]() ʱ�����о������S=
ʱ�����о������S= ![]() ��
��
��ɲ����������ʻ�� ![]() �ײ�ֹͣ��
�ײ�ֹͣ��
�ڡ�s=��5t2+15t����s1=��5t12+15t1��s2=��5t22+15t2
�� ![]() =��5t1+15��
=��5t1+15��
ͬ�� ![]() =��5t2+15��
=��5t2+15��
��t1��t2��
�� ![]() ��
�� ![]() ��
��
��ʵ��������ɲ����t2ʱ���ڵ�ƽ���ٶ�С��ɲ����t1ʱ���ڵ�ƽ���ٶ�
����������1����㣬��ƽ���������Ӽ��ɣ���2��������κ�������ʽ����3������������ɵö��κ�������ʽ�������ٰ�����ĵ������֤�Ƿ��ڶ��κ����ϣ���3����������ɲ��ʱ���ʱֹͣ�����ù�ʽ������ϣ�2���õ��ĺ�������ʽ�������Ӧ����ֵ���ɣ��ڷֱ������������ʽ��ֵ����������ʱ��Ĵ�С���Ƚϼ��ɣ�


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB=10��AC=BD=2����P��CD��һ���㣬�ֱ���AP��PBΪ�����ϡ�������������APEF��PHKB���������ζԽ��ߵĽ���ֱ�ΪO1��O2 �� ����P�ӵ�C�˶�����Dʱ���߶�O1O2�е�G���˶�·���ij��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���������C1��y=x2+3������ƽ��1����λ��������ƽ��7����λ�õ�������C2 �� C2��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��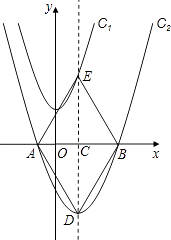
��1����������C2�Ľ���ʽ��
��2����������C2�ĶԳ�����x�ύ�ڵ�C����������C2���ڵ�D����������C1���ڵ�E������AD��DB��BE��EA����֤���ı���ADBE�����Σ����������������
��3������FΪ�Գ���DE������һ�㣬��������C2���Ƿ���������ĵ�G��ʹ��O��B��F��G�ĵ�Ϊ������ı�����ƽ���ı��Σ�������ڣ��������G�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ���װ�к졢�ơ���������ɫ��100�������dz���ɫ�ⶼ��ͬ�����л�������ǰ��������2����5������֪�Ӵ�������һ�����Ǻ���ĸ����� ![]() ��
��
��1������к���ĸ�����
��2����Ӵ�������һ�����ǰ���ĸ��ʣ�
��3��ȡ��10��������û�к������ʣ�����������һ�����Ǻ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��������ֽƬABC�У�AB=3��AC=4��DΪб��BC�е㣬��1�ν�ֽƬ�۵���ʹ��A���D�غϣ��ۺ���AD���ڵ�P1����P1D���е�ΪD1 �� ��2�ν�ֽƬ�۵���ʹ��A���D1�غϣ��ۺ���AD���ڵ�P2����P2D1���е�ΪD2 �� ��3�ν�ֽƬ�۵���ʹ��A���D2�غϣ��ۺ���AD���ڵ�P3��������Pn��1Dn��2���е�ΪDn��1 �� ��n�ν�ֽƬ�۵���ʹ��A���Dn��1�غϣ��ۺ���AD���ڵ�Pn��n��2������AP6�ij�Ϊ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ���E��F��AB���ϣ�����DE��CF��AD��G����E��BF�е㣮
��1����֤����AFG�ס�AED
��2����FG=2��GΪAD�е㣬��CG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������е����Ļ�վA��B��վ���360 km.һ�ж�����һ���ؿ��г��ֱ��A��B��վͬʱ����������У�������ƽ���ٶȱ��ؿ��г���54 km/h������������Bվʱ���ؿ��г�ǡ�õ������Aվ135 km����Cվ�������ؿ��г���ƽ���ٶȸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
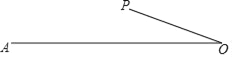
����Ŀ����ͼ���߶�OA��2��OP��1�����߶�OP�Ƶ�O������תʱ���߶�AP�ij���Ҳ��֮�ı䣬�����н��ۣ�
��AP����Сֵ��1�����ֵ��4��
����AP��2ʱ����APO�ǵ��������Σ�
����AP��1ʱ����APO�ǵ��������Σ�
����AP��![]() ʱ����APO��ֱ�������Σ�
ʱ����APO��ֱ�������Σ�
����AP��![]() ʱ����APO��ֱ�������Σ�
ʱ����APO��ֱ�������Σ�
������ȷ����(����)
A. �٢ܢ� B. �ڢۢ� C. �ڢܢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com