
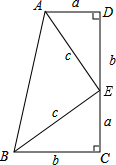
 如图,已知∠C=∠D=90°,D,E,C三点共线,各边长如图所示,请利用面积法证明勾股定理.
如图,已知∠C=∠D=90°,D,E,C三点共线,各边长如图所示,请利用面积法证明勾股定理. 分析 先利用“边角边”证明△ADE和△EBC全等,根据全等三角形对应角相等可得∠AED=∠CBE,再求出∠AEB=90°,然后根据梯形的面积公式和梯形的面积等于三个直角三角形的面积列出方程整理即可得证.
解答 证明:在△ADE和△EBC中,$\left\{\begin{array}{l}{AD=EC}\\{∠C=∠D=90°}\\{DE=BC}\end{array}\right.$,
∴△ADE≌△EBC(SAS),
∴∠AED=∠CBE,
∵∠CBE+∠BEC=90°,
∴∠AED+∠BEC=90°,
∴∠AEB=90°,
∴梯形的面积=$\frac{1}{2}$(a+b)(a+b)=2×$\frac{1}{2}$ab+$\frac{1}{2}$c2,
整理得,a2+b2=c2.
点评 本题考查了勾股定理的证明,全等三角形的判定与性质,求出∠AEB=90°是解题的关键,难点在于利用梯形的面积列出方程.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
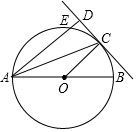 如图,AB是⊙O的直径,点C为⊙O上一点,AD和过C点切线交于点D,和⊙O相交于E,且AC平分∠DAB.
如图,AB是⊙O的直径,点C为⊙O上一点,AD和过C点切线交于点D,和⊙O相交于E,且AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-y2=1 | B. | $\sqrt{{x}^{2}-1}$=0 | C. | $\frac{1}{{x}^{2}}$-1=0 | D. | $\frac{{x}^{2}}{2}$+$\frac{x}{3}$-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com