
【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.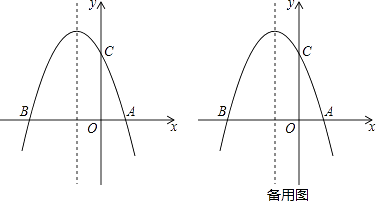
(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
【答案】
(1)
解:将A(2,0),B(﹣4,0)代入得:
![]() ,
,
解得: ![]() ,
,
则该抛物线的解析式为:y=﹣x2﹣2x+8
(2)
解:如图1,点A关于抛物线对称轴的对称点为点B,设直线BC的解析式为:
y=kx+d,
将点B(﹣4,0)、C(0,8)代入得:
![]() ,
,
解得: ![]() ,
,
故直线BC解析式为:y=2x+8,
直线BC与抛物线对称轴 x=﹣1的交点为Q,此时△QAC的周长最小.
解方程组 ![]() 得,
得, ![]()
则点Q(﹣1,6)即为所求

(3)
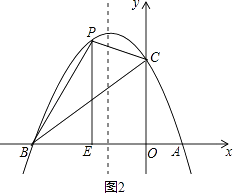
解:如图2,过点P作PE⊥x轴于点E,
P点(x,﹣x2﹣2x+8)(﹣4<x<0)
∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣16
若S四边形BPCO有最大值,则S△BPC就最大
∴S四边形BPCO=S△BPE+S直角梯形PEOC
= ![]() BEPE+
BEPE+ ![]() OE(PE+OC)
OE(PE+OC)
= ![]() (x+4)(﹣x2﹣2x+8)+
(x+4)(﹣x2﹣2x+8)+ ![]() (﹣x)(﹣x2﹣2x+8+8)
(﹣x)(﹣x2﹣2x+8+8)
=﹣2(x+2)2+24,
当x=﹣2时,S四边形BPCO最大值=24,
∴S△BPC最大=24﹣16=8,
当x=﹣2时,﹣x2﹣2x+8=8,
∴点P的坐标为(﹣2,8).
【解析】(1)直接利用待定系数求出二次函数解析式即可;(2)首先求出直线BC的解析式,再利用轴对称求最短路线的方法得出答案;(3)根据S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣16,得出函数最值,进而求出P点坐标即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
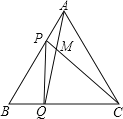
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的有( )
①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
③三角形的三边分别为a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
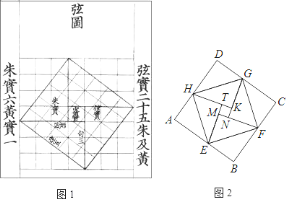
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图![]() ),图
),图![]() 由弦图变化得到,它是由作个全等的直角三角形拼接而成,记图中正方形
由弦图变化得到,它是由作个全等的直角三角形拼接而成,记图中正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的值是( )
的值是( )
A. 5 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,有![]() 张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是( )
张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学研究课上,老师出示如图1所示的长方形纸条![]() ,
,![]() ,
,![]() ,然后在纸条上任意画一条截线段
,然后在纸条上任意画一条截线段![]() ,将纸片沿
,将纸片沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,得到
,得到![]() ,如图2所示:
,如图2所示:

(1)若![]() ,求
,求![]() 的大小;
的大小;
(2)改变折痕![]() 位置,判断
位置,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)爱动脑筋的小明在研究![]() 的面积时,发现
的面积时,发现![]() 边上的高始终是个不变的值.根据这一发现,他很快研究出
边上的高始终是个不变的值.根据这一发现,他很快研究出![]() 的面积最小值为
的面积最小值为![]() ,求
,求![]() 的大小;
的大小;
(4)小明继续动手操作,发现了![]() 面积的最大值,请你求出这个最大值.
面积的最大值,请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C,D同时出发,当动点D到达原点O时,点C,D停止运动.
(1)直接写出抛物线的解析式:;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com